4.3.2.2 Расчет надежности при общем и раздельном резервировании систем

Общее резервирование с постоянно включенным резервом (см. рисунок 4.11). Допущения:

1) отказы элементов системы описываются простейшим потоком отказов;

2) резервируемые и резервные элементы равнонадежны.

Задано:

1) число основных элементов в системе N;

2) ВБР j-го элемента;

3) кратность резервирования.

Требуется определить характеристики надежности резервированной системы.

ВБР системы с последовательной схемой соединения элементов без резервирования при независимых отказах равна 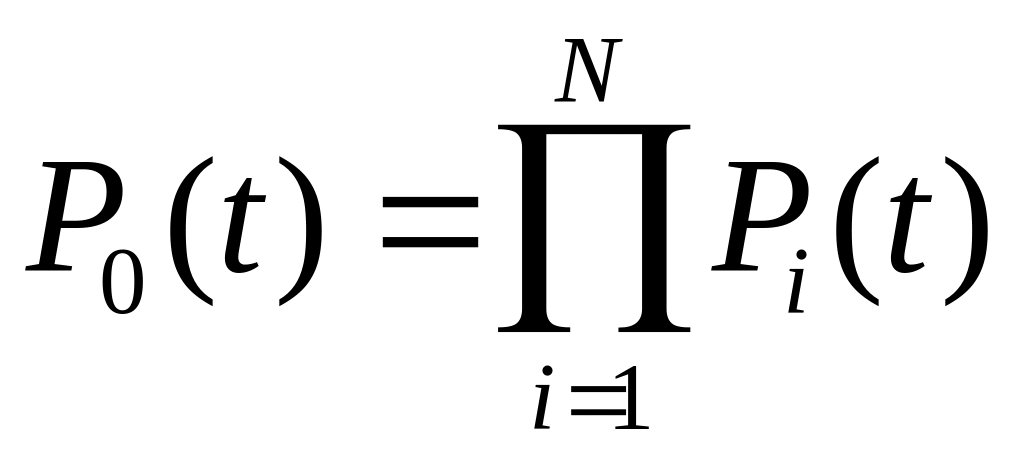[14]

, (4.14)

а вероятность отказа

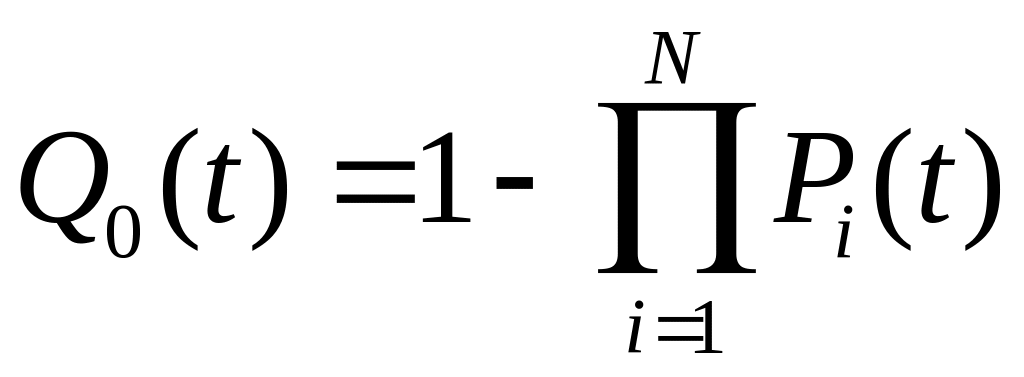. (4.15)

Для экспоненциального закона надежности

(4.16)

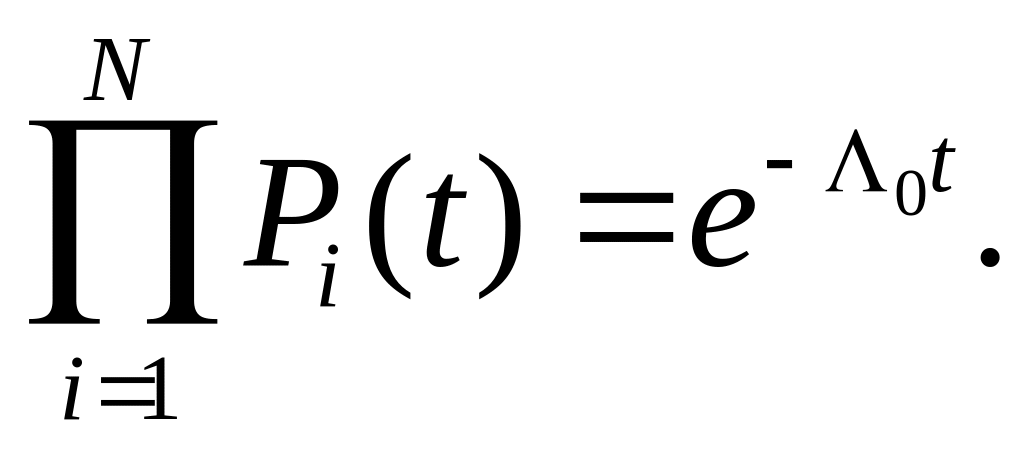(4.17)

4.3.2.3 Расчет надежности при резервировании систем с дробной кратностью

Будем рассматривать случай резерви­рования системы с дробной кратностью и нагруженным резервом (рисунок 4.18) [3].

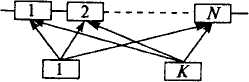
Рисунок 4.18 – Резервирование с дробной кратностью при нагруженном резерве

При резервировании с дробной кратностью нормальная работа резервирован­ного соединения возможна при условии, если число исправных элементов не мень­ше необходимого для нормальной работы.

Кратность резервирования определя­ется из соотношения

(4.18)

где Z – общее число элементов расчета резервированного соединения;

N – число элементов, необходимое для нормальной работы соединения;

Z-N — число резервных элементов.

Пусть резервированная система состоит из N основных и К резервных элементов (N> К). При отказе одного из основных элементов, на его место без перерыва в работе включается один из резервных (резервные элементы также могут отказывать). Таких замещений, не нарушающих работу резервированной системы в целом, не может быть больше К. Средняя наработка до отказа такой резервированной системы в предположении абсолютно надежных переключающих устройств и равнонадежных элементов с интенсивностью отказов каждого λ равна

(4.19)

Безотказная работа системы в течение времени t будет иметь место, если за это время осуществится хотя бы одна из гипотез: Н_о — все элементы исправны; H₁ — один элемент отказал, (К + N — 1) элементов исправны; (H_i - i) элементов отказали, (К+N-i) элементов исправны; (Н_к - К) элементов отказали, N элементов исправны. Число различных вариантов равно

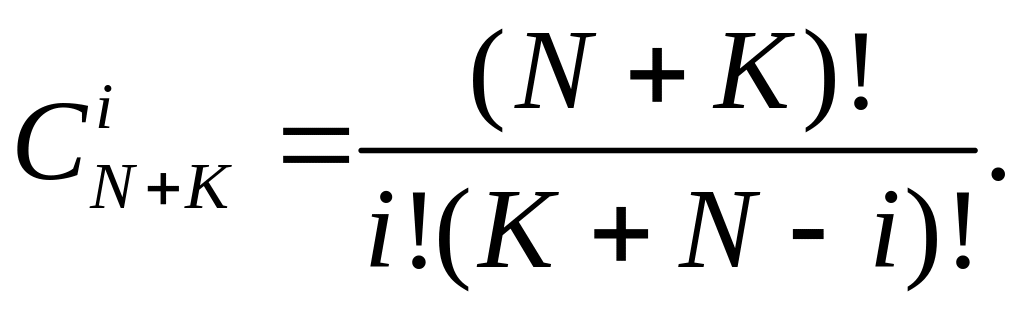(4.20)

Тогда ВБР системы можно определить из выражения

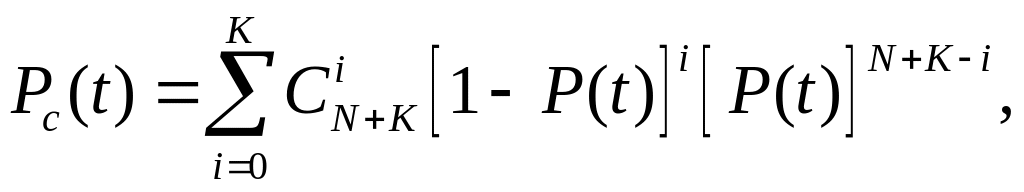(4.21)

где P(t) — вероятность безотказной работы элемента при условии, что все элементы равнонадежны. Для мажоритарного резервирования по схеме «2 из 3» вероятность безотказной работы системы можно подсчитать по формуле

(4.22)

где P(t) — ВБР одного канала (элемента, подсистемы); P_M(t) — ВБР мажоритарного органа.