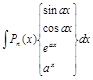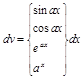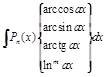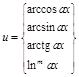3.3. Метод інтегрування частинами

Нехай   та   – деякі неперервно диференційовні функції. Відомо, що диференціал від добутку функцій запишеться  , звідки  . Інтегруючи обидві частини цієї рівності, отримаємо  .                                                           (3.4) Ця формула називається формулою інтегрування частинами, вона зводить інтегрування виразу   до інтегрування виразу  . Щоб застосувати формулу інтегрування частинами, необхідно підінтегральний вираз розділити на два множники, один з яких позначимо через  , а інший –  . Тоді:

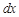•  повинен бути віднесений до  ;

• вираз   треба вибирати так, щоб легко можна було знайти функцію 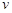 , оскільки 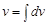  (сталу   не додавати – можна вважати, що  );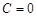

• як   вибираємо ту функцію з підінтегрального виразу, що після диферен­ціювання спрощується.

Метод інтегрування частинами зручно використовувати, якщо підінтегральна функція містить:

• добутки функцій    ,  ;

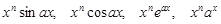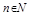• деякі вирази, в які входять логарифмічні та обернені тригонометричні функції;

• деякі інші функції, зокрема вигляду       .

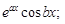
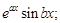
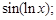
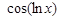Детальніші рекомендації подано в табл. 4.

Таблиця 4

№	Вигляд  інтеграла	Множник	Множник	Зауваження
1				разів інтегруємо частинами, кожен раз вибираючи за   многочлен  .
2
3		Можливий довільний вибір		Інтегруємо частинами двічі, причому при другому інтегруванні робимо аналогічне розбиття на   і   (див. прикл. 3.8.).
4				Двічі інтегруємо частинами.

(Тут   – многочлен степеня   відносно  ). Застосовуючи формулу інтегрування частинами, не одразу знаходимо первісну, а цей інтеграл зводимо до іншого, і якщо цей інтеграл простіший від заданого, то формула вжита правильно.

Приклад 3.6. Знайти інтеграл  .

• Нехай 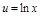 ;  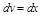, тоді  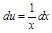;  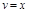 і, згідно з (3.4), отримаємо  .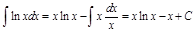

Повторне використання інтегрування частинами. Іноді формулу інтегрування частинами необхідно застосовувати декілька разів (див. табл. 4).

Приклад 3.7.  Визначити інтеграл  .  á   Проінтегруємо частинами, двічі кожен раз вибираючи за   многочлен, за  – вираз   (див. табл. 4). (Зауважимо, що після кожного інтегрування степінь многочлена під знаком інтеграла понижується на одиницю)  .

Повернення до вихідного інтеграла. Іноді повторне використання формули інтегрування частинами приводить до рівняння щодо шуканого інтеграла. Продемонструємо це на прикладі.

Приклад 3.8.  Знайти інтеграл  .  á Проінтегруємо частинами двічі, вибираючи, наприклад, як   тригонометричну функцію,  як   – вираз ,  .  Отже, одержали  рівняння щодо невідомого інтеграла  ,  звідки, переносячи інтеграли у ліву частину рівності і враховуючи сталу інтегрування  ,  матимемо   .  Отже,   .

Рекурентні формули. Іноді інтегрування частинами дає змогу отримати співвідношення між невизначеним інтегралом, що містить степінь деякої функції, і аналогічним інтегралом, але з меншим показником степеня тієї самої функції. Такі співвідношення називаютьрекурентними формулами. Прикладом такої формули, що буде застосовуватись у наступному розділі і може бути доведена інтегруванням частинами, є  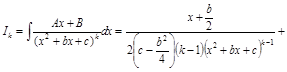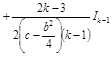,      ( ).                                             (3.5)