1. Означення та властивості невизначеного інтеграла  1.1. Первісна. Невизначений інтеграл З попередніх розділів відомо, що основним завданням диференціального числен­ня є визначення похідної чи диференціала заданої функції  .  Розглянемо обернену задачу: для заданої функції   знайти таку функцію  , похідна якої збігалася б з цією функцією, тобто   або  . Наприклад, якщо  , то легко здогадатись, що  .

Означення 1.1.Функція   називається первісною функції   на інтервалі  , якщо для будь-якої точки   функція   диференційовна і задовольняє умову      або     .                                    (1.1)  Інтервал  може бути скінченним або нескінченним.

Очевидно, що якщо для функції існує первісна, то вона не є єдиною. Так, у наведеному прикладі первісними функції   є  ,  , чи, загалом, сім'я функцій   , де  – довільна стала.

Теорема 1.1.Якщо функція   має дві первісні   і   на інтервалі  , то вони відрізняються між собою на стале число: .

Геометрична інтерпретація теореми 1.1.Якщо   та   – первісні однієї і тієї самої функції  , то величина  , яка є відстанню між цими кривими вздовж осі  , залишається сталою:  , тобто ці криві в певному розумінні "паралельні" між собою (рис. 1).

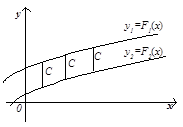  Рис.1. Сім'я первісних 

Як випливає із теореми 1.1, якщо відома хоча б одна первісна  , то одно­параметричну сім'ю  усіх первісних отримують, додаючи довільну сталу:  .

Означення 1.2.Сукупність усіх первісних заданої функції   на інтервалі   називається невизначеним інтегралом функції   і позначається символом  .

Якщо   – яка-небудь первісна   на інтервалі  , то пишуть .                                                        (1.2) Функція   називається підінтегральною функцією;  – підінтегральним виразом;  – знак інтеграла;  – довільна стала. Зауважимо, що під знаком інтеграла " " записують диференціал шуканої функції, а не похідну. Такий спосіб запису склався історично; він має певні переваги, які будуть пояснені далі:  Визначення для функції усіх її первісних, що називається інтегруванням, і є одним з основних завдань інтегрального числення. Правильність знаходження інтеграла легко перевірити оберненою операцією диференціювання.

Теорема 1.2.Якщо функція неперервна на інтервалі  , то для неї існує первісна та невизначений інтеграл.

Надалі будемо говорити про первісні та інтеграли лише для неперервних функцій. Якщо ж функція має точки розриву, то її розглядатимемо лише на проміжках неперервності.

2. Основні властивості невизначеного інтеграла та правила інтегрування 2.1. Основні властивості невизначеного інтеграла

• Диференціал невизначеного інтеграла дорівнює підінтегральному виразу, тобто

.                                                    (2.1)

• Невизначений інтеграл від диференціала функції дорівнює сумі функції та довільної сталої, тобто

,                                                      (2.2) де  – неперервно диференційовна функція.

Слід зазначити: з першої властивості випливає, що комбінація символів  , застосована до виразу  , взаємно знищується, а з другої – що комбінація символів  , використана до функції  , додає до цієї функції сталу  .

• Таблиця основних інтегралів

Кожна формула диференціального числення, яка показує, що для деякої функції   існує похідна  , безпосередньо приводить до відповідної формули інтегрального числення  . На підставі таблиці похідних запишемо таблицю інтегралів (її справедливість легко перевірити диференціюванням: похідна від правої частини рівностей збігається з підінтегральною функцією).

Таблиця 1 Основні інтеграли

      1)  ;                                                               9)  ; 2)  ;                                                           10)  ;  3)  ;                             11) 4)  ;                                                            ;  5)  ;                                                     12)  ; 6)  ;                                                 13)  7)  ;                                                ;    8)  ;                                           14)  .  Доповнимо цю таблицю ще двома інтегралами, які часто використовуються. 15)  ;          16)  .  Інтеграли, що знаходять безпосередньо із застосуванням формул 1–16, називаються табличними.  Приклад 2.1.Знайти інтеграли:   а)  ;   б)  . á  а) Перетворимо підінтегральну функцію   і скористаємось формулою 3  табл. 1  якщо  . Отже,  . б) Цей інтеграл можна знайти згідно з формулою 12 табл. 1 якщо  :  .

• Основні правила інтегрування

 

Теорема 2.1. Сталий множник можна виносити за знак інтеграла, тобто  .                                                                                       (2.3)

Приклад 2.2.Обчислити інтеграл  .  á   Винесемо сталий множник   за знак інтеграла та використаємо табл.1: .

Теорема 2.2.Невизначений інтеграл від алгебраїчної суми скінченної кількості функцій дорівнює алгебраїчній сумі невизначених інтегралів від кожної із функцій -доданків. Тобто якщо функції  ,  ,  – неперервні на  , то на цьому інтервалі .                            (2.4)

Приклад 2.3.Знайти   . á   Перетворимо підінтегральну функцію і використаємо по черзі властивості (2.4), (2.3):   . Зауваження.Немає потреби після кожного доданка записувати сталу інтегрування, адже сума довільних сталих є також сталим значенням, яке ми врахували в кінці і позначили  .

Приклад 2.4.Граничний дохід фірми описується функцією  , де  – кількість виробленої продукції. Якою буде функція  загального доходу фірми, якщо нульовий випуск продукції дає нульовий дохід? á   Згідно з означенням граничного доходу загальний дохід становить  . Із сукупності первісних   виберемо ту, для якої виконується умова нульового доходу за нульового випуску продукції  :  , звідки  . Отже, сумарний дохід фірми описується функцією  .