13. Инварианты напряженного состояния. Интенсивность напряжений. Наибольшие касательные напряжения.

Г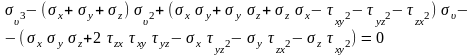 лавные напряжения являются корнями кубического уравнения (подробности получения его опускаем):

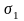
М аксимальное главное напряжение (в алгебраическом смысле) –

Минимальное главное напряжение –

З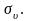 начения корней кубического уравнения зависят от коэффициентов, стоящих при различных степенях

В свою очередь, значения этих коэффициентов не зависят от выбора системы координат:

они инвариантны к системе координат.

Их называют: инварианты напряженного состояния S

(соответственно, первый, второй, третий инварианты):

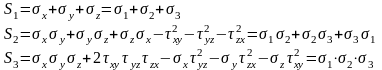
Тогда кубическое уравнение примет вид:

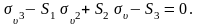
Интенсивность напряжений

В сопромате и теории упругости при проведении расчетов используются так называемые теории прочности (будут рассмотрены ниже).

При разработке этих теорий вводится гипотеза о преимущественном влиянии на прочность материала того или иного фактора (критерия). Таким образом, предусматривается возможность проверки этого критерия сопоставлением данного (сложного) напряженного состояния с простым (обычно с одноосным).

П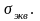 ри этом устанавливается значение эквивалентного (расчетного) напряжения

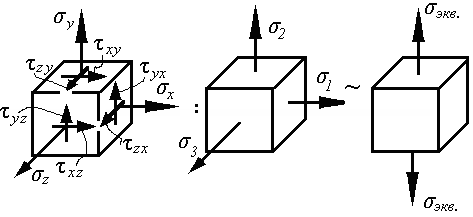
В теории упругости эквивалентные напряжения называют интенсивностью напряжений

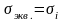
Наибольшие касательные напряжения

Анализ напряженных состояний позволяет определить величину максимальных касательных напряжений.

Эти напряжения (доказано в теории упругости и подтверждается экспериментально) «ответственны» за пластическую деформацию тела.

М аксимальное значение касательных напряжений определяется полуразностью экстремальных значений главных напряжений:

14.Выражение копмонентов деформаций через перемещения(состояние Коши)

________________________________________________________________________________

Сопротивление материалов и теория упругости перемещения отдельных точек тела связывают с его деформациями.

Причем, в теории упругости решается задача получения в общей форме геометрических зависимостей деформаций от напряжений в нагруженном теле.

При деформации, точки тела перемещаются. Например, точка А (x, y, z) переместится в точку в А₁, т.е. получит перемещения u, v, w.

К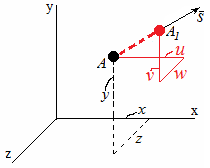 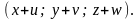оординаты точки А₁:

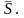
Отрезок АА₁ есть модуль полного перемещения

Поле напряжений в нагруженном теле является неоднородным, поэтому поле деформаций также будет неоднородным.

Воспользуемся также тем обстоятельством, что даже большие величины напряжений сопровождаются весьма малыми деформациями:

деформации малы по сравнению с размерами тела.

Следовательно, при переходе от точки А к точке А₁ величины деформаций бесконечно малых отрезков, параллельных координатным осям, будут изменяться на величину дифференциала.

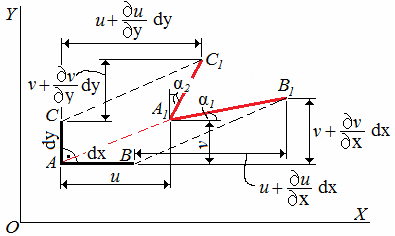
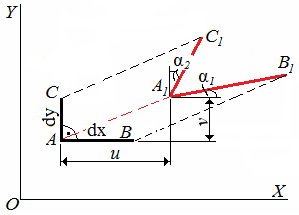
В ыделим в теле два отрезка АВ и АС бесконечно малой длины (dx, dy) с прямым углом между ними.

После деформации тела точки А, В, С переместятся в новое положение

Относительная линейная деформация

И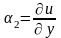 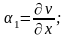зменение углов:

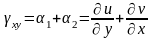
относительная угловая деформация

О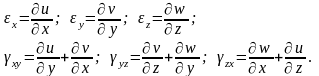 кончательные выражения для относительных линейных и угловых деформаций для всех трех координатных плоскостей называют соотношениями Коши: