1 2. Тензор напряжений и его составляющие. Главные площадки и главные напряжения. Виды напряженных состояний.

Матрицу напряжений называют тензором. Обозначают Т_σ.

Тензор напряжений описывает напряженное состояние в точке.

Запишем среднее от суммы нормальных напряжений

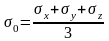
Среднее напряжение

Т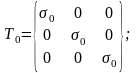 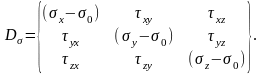огда любое напряженное состояние, описываемое тензором напряжений Т_σ, можно представить суммой двух НС:

Шаровой тензор Т₀ – характеризует НС, отвечающее всестороннему сжатию или растяжению, которое приводит только к изменению объема.

Девиатор D_σ – характеризует НС, приводящее только к изменению формы.

Главные напряжения и главные площадки

При изменении положения выделенного элемента (при его повороте в пространстве)

Теория упругости доказывает, что всегда можно найти такое положение элемента, при котором на его гранях касательные напряжения будут отсутствовать, т.е. равняться нулю.

Площадки, по которым не действуют касательные напряжения, называются главными площадками.

Экстремальные нормальные напряжения σ на этих площадках – главные напряжения.

В теории упругости также доказывается, что в каждой точке любым образом нагруженного тела всегда имеются

три главные взаимно перпендикулярные площадки.

Главные напряжения принято обозначать

σ₁, σ₂, σ₃,

при этом полагают, что в алгебраическом смысле: σ₁ > σ₂ > σ₃

Виды напряженных состояний

Вид напряженного состояния определяется

количеством действующих главных напряжений.

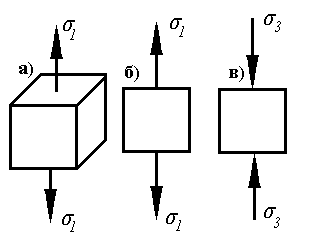
1). Линейное (одноосное) напряженное состояние

К граням элементарного параллелепипеда приложено только одно нормальное напряжение.

Остальные два равны нулю.

Если нормальное напряжение растягивающее – имеем наибольшее главное напряжение σ₁ (рис. а).

Схемы на рис. а и рис. б аналогичны – во втором случае вместо параллелепипеда изображена одна плоская грань.

На рис. в – приложено только одно сжимающее нормальное напряжение, поэтому обозначаем его σ₃.

2) Плоское (двухосное) напряженное состояние

По любым двум взаимно перпендикулярным граням параллелепипеда (в нашем случае по граням произвольного плоского элемента) могут быть приложены два одинаковых по величине и направлению нормальных напряжения.

Если оба растягивающих (рис. а), то обозначаем их σ₁ и σ₂ ,(σ₃=0 ),

если оба сжимающих (рис. б), то σ₂ и σ₃, (σ₂=0).

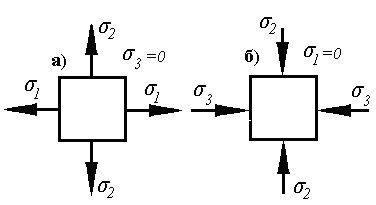
Но может быть и вариант (рис. в).

В этом случае одно нормальное напряжение растягивающее, другое – сжимающее.

Наибольшее по величине (в алгебраическом смысле) нормальное напряжением обозначается σ₁ наименьшее σ₃ σ₂=0.

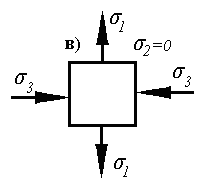
3) Объемное (трехосное) напряженное состояние

В этом случае вариантов приложения напряжений еще больше.

Подходы к обозначениям главных напряжений рассмотрены достаточно подробно выше.

В большинстве случаев в инженерных расчетах встречаются линейное или плоское напряженные состояния.

З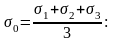 апишем выражения для шарового тензора и девиатора через главные напряжения, обозначив

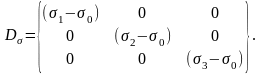
Руководствуясь принципом суперпозиции, покажем схемы напряженных состояний, определяющих, соответственно, изменение объема и изменение формы элементарного параллелепипеда.