8. Диаграммы упругопластического деформирования конструкционных материалов
____________________________________________________________________________________
Используются для анализа поведения и определения характеристик конструкционных материалов.
Пластичность – свойство материала претерпевать значительные остаточные деформации перед разрушением без нарушения сплошности и образования трещин.
Вязкость – свойство материала поглощать механическую энергию в пластически деформируемых объемах без снижения прочности.
Диаграммы деформирования
Механические характеристики материалов – числовые значения, характеризующие прочность, жесткость, пластичность, упругость, вязкость и другие свойства. Они определяются экспериментально, на основе результатов испытаний образцов: по диаграммам деформирования.
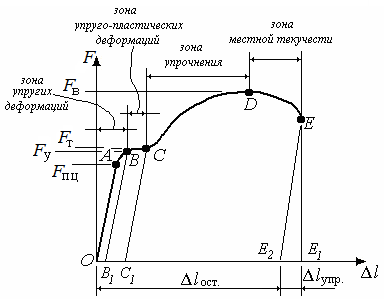
Машинную диаграмму деформирования при определении механических характеристик материалов перестраивают в системе координат: напряжение – относительная деформация.
Вид диаграммы остается прежним.
При растяжении образца
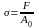
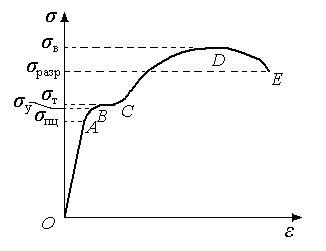
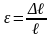
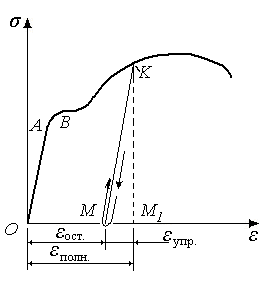
Закон разгрузки и повторного нагружения
У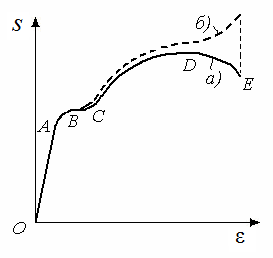
словная
(а)
и истинная (б)
диаграммы растяжения
9.Анизотропия механических свойств материалов.
Одно из основных допущений сопромата и теории упругости – изотропия материала.
Большинство материалов и изделий из них имеют анизотропию механических свойств.
В расчетах обычно анизотропию не учитывают.
Характерный материал с анизотропией – дерево:
имеет разные механические свойства вдоль и поперек волокна.
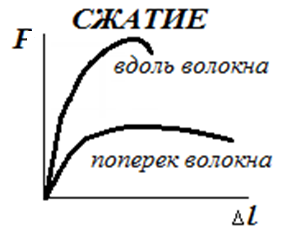
Различают:
НАЧАЛЬНУЮ ИЛИ ИСХОДНУЮ анизотропию – существует до нагружения (например, анизотропия свойств монокристаллов);
ВТОРИЧНУЮ ИЛИ ДЕФОРМАЦИОННУЮ анизотропию – изменившуюся или возникшую в процессе деформации (в результате прокатки, прессования, волочения, ковки).
РАЗРУШЕНИЕ на всех стадиях ведет к анизотропии.
Измеряется в МПА
Влияние анизотропии следует учитывать при проектировании конструкций:
трубы и емкости, работающие под давлением изготавливают из листа при ориентировании максимальной прочности по окружности, т.к.
осевые (меридиональные) напряжения в 2 раза меньше тангенциальных (окружных):
для повышения прочности бетона при растяжении – армирование плит стальной арматурой (железобетонные плиты);
при исследованиях, например, сварных соединений, образцы вырезают в различных зонах и направлениях:
вдоль и поперек сварного шва,
в околошовной зоне,
в основном металле,
из всего сварного соединения
10. Ответ не найдет!
11. Напряжения на наклонных площадках и условия на поверхности.
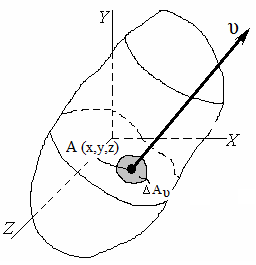
При решении различных задач требуется определить величину и направление компонент напряжений по площадкам, наклоненным к координатным осям, а также величину и направление компонент напряжений на поверхности тела. При этом, у поверхности выделить элементарный параллелепипед не представляется возможным.
В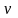
округ
некоторой произвольной точки А (x,
y,
z)
, расположенной внутри тела, нагруженного
внешними силами, выделена площадка ∆А
произвольной формы с нормалью .
П
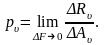
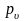о
элементарной площадке действует
равнодействующая внутренних сил ∆R
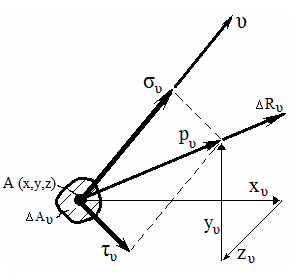
Полное напряжение
е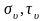
го
составляющие:
П роекции полного напряжения на координатные оси: x , y , z .
Рассечем параллелепипед наклонной плоскостью, пересекающей координатные оси в точках В, С, D.
Получили наклонную площадку ∆Аυ, нормаль к которой υ.
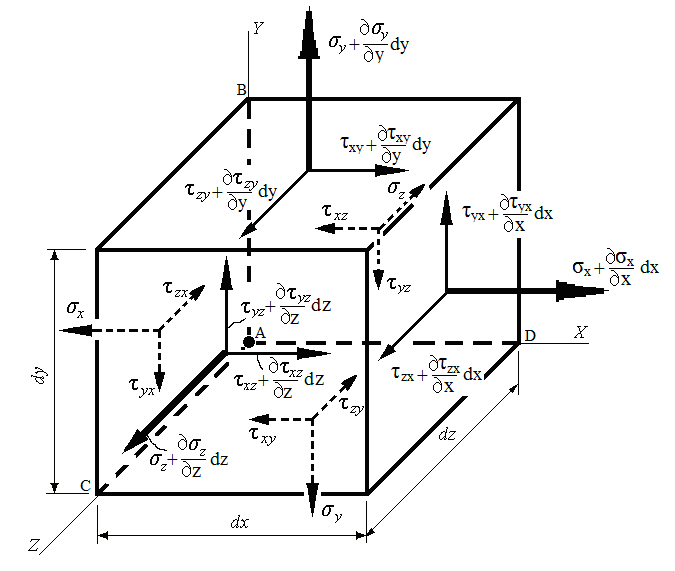
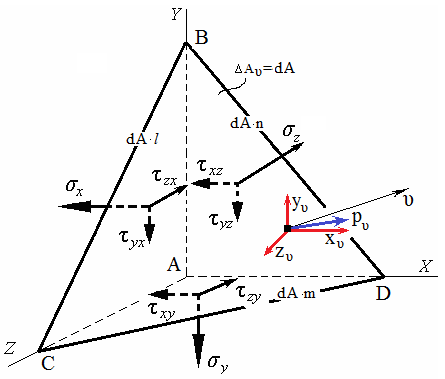
Положение наклонной площадки определяется углами (направляющими косинусами) между нормалью и соответствующими осям координат.
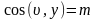
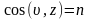
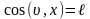
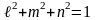
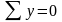
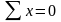
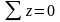
Уравнения равновесия
Произведением объемных сил пренебрегаем
(величина третьего порядка малости).
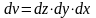
Уравнения, по которым определяются компоненты напряжений, действующих на произвольной поверхности с нормалью υ:
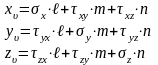
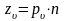
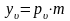
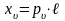
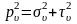
Условие на поверхности
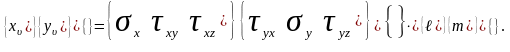Запись
условий на поверхности в матричной
форме