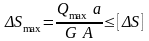4.Прямой изгиб бруса. Зависимость между изгибающим моментом и кривизной оси прямого бруса.Формула Навье.Условие прочности.

______________________________________________________________________________________

Прямой изгиб бруса

Виды изгиба

Изгиб – вид нагружения (деформации)

бруса, при котором в его поперечных сечениях

действуют изгибающие моменты.

Брус с прямой осью называется стержнем.

Стержни, работающие на изгиб, называют балками.

При изучении изгиба будем рассматривать лишь такие балки, сечения которых имеют одну или две оси симметрии, а действующие внешние силы лежат в одной из плоскостей симметрии.

С видами нагрузок, типами опор, видами балок и определением внутренних силовых факторов мы познакомились ранее.

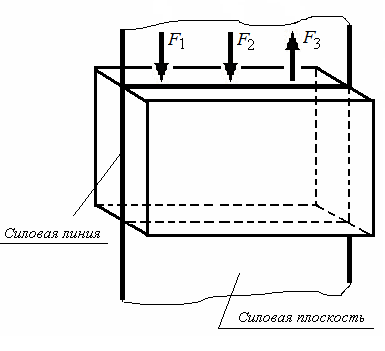
Линия пересечения силовой плоскости с плоскостью поперечного сечения балки – силовая линия.

Плоскость действия внешних сил – силовая плоскость

А). Если в сечениях действуют только изгибающие моменты, то такой вид изгиба называют чистым.

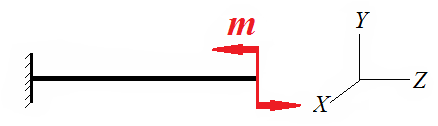
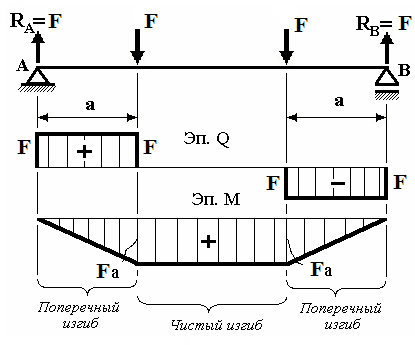
Б). В большинстве случаев одновременно с изгибающими

моментами возникают и поперечные силы. Такой вид изгиба называют поперечным

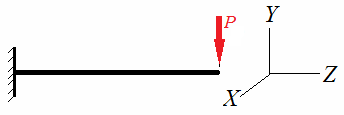
Зависимость между изгибающим моментом и кривизной нейтральной оси прямого бруса

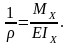
ρ – радиус кривизны нейтрального слоя.

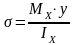
Нормальные напряжения:

Формула НАВЬЕ

Условие прочности по нормальным напряжениям

Ранее был сделан вывод о том, что максимальные напряжения возникают в слоях, наиболее удаленных от нейтрального слоя.

Максимальные нормальные напряжения:

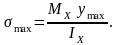
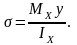
осевой момент сопротивления сечения

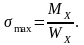
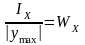
У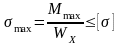 словие прочности по нормальным напряжениям

Момент сопротивления сечения определяем относительно оси, перпендикулярной силовой плоскости.

С использованием условия прочности выполняются

3 вида расчетов:

1. проверка прочности

2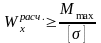 . проектировочный расчет

(подбор размеров сечения балки)

3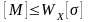 . расчет максимальной грузоподъемности

(допускаемые значения внешних нагрузок)

5.Сдвиг.Определение касательных напряжений. Закон Гука. Определение перемещений. Условие прочности

Расчеты на прочность и жесткость при сдвиге (срезе)

В расчётах деталей машин часто приходится иметь дело с различными соединениями этих деталей, в которых элементы испытывают сдвиг (заклепочные и болтовые соединения, сварные соединения).

Разрушение от сдвига обычно называют срезом.

Сдвигом называют вид нагружения бруса, в поперечном сечении которого возникает только поперечная сила Q_X или Q_Y.

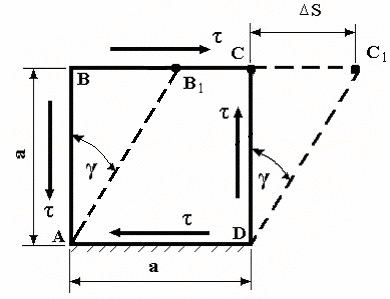
С достаточной степенью приближения сдвиг может быть получен в случае, когда на рассматриваемый брус с противоположных сторон на весьма близком расстоянии друг от друга действуют две равные силы, перпендикулярные к оси бруса и направленные навстречу друг другу.

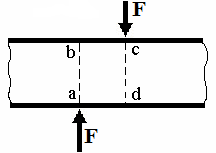
При этом участок бруса между точками приложения силы сдвигается – приняв сечение аb неподвижным, получим смещение сечения cd в положение c₁d₁. Если расстояние между сечениями будет близким к нулю, эти сечения будут скользить друг по другу.

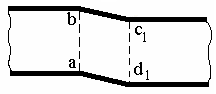
Пример: резка ножницами прутьев, полосы и т.д., при условии, что сечения, в которых прикладываются силы, расположены очень близко друг к другу.

Если это условие не выполняется, то в сечениях появится изгибающий момент, определяемый силой, умноженной на плечо (расстояние между точками приложения сил).

Однако, для очень короткого бруса, влияние изгиба будет незначительно и поэтому им можно пренебречь. Таким образом, получим действие только поперечной силы, т.е. сдвиг.

Рассечем брус сечением I-I и отбросим его левую часть.

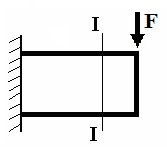
О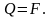 чевидно, что действие отброшенной части на оставшуюся часть бруса будет выражаться через внутреннюю силу

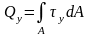
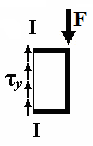
Для упрощения решения практических задач предполагается, что касательные напряжения при сдвиге распределяются по сечению равномерно. Нормальные напряжения равны нулю.

К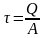 асательные напряжения при сдвиге

У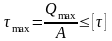 словие прочности при сдвиге:

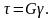
Закон Гука:

G – модуль упругости II рода (модуль сдвига)

абсолютный сдвиг:

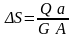
Условие жесткости: