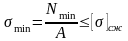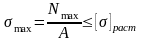2. Метод расчета конструкций по допускаемым напряжениям. Критерии прочности и разрушения материалов.

------------------------------------------------------------------------------------------------------------------------------------

При применении этого метода величина максимальных рабочих напряжений в опасном сечении бруса (или в наиболее нагруженных элементах конструкции) ограничивается так называемыми допускаемыми напряжениями Рассматриваемый метод расчета основан на сравнении опасных нагрузок с фактическими нагрузками, действующими на сооружение.

Следовательно, нам необходимо знать величину этих опасных нагрузок, которые будут характеризоваться предельным состоянием материала – состоянием, при котором происходит разрушение или наблюдаются пластические деформации.

Критерии наступления предельного состояния устанавливаются экспериментально при испытаниях образцов:

для пластичных материалов опасным является предел текучести;

для хрупких материалов – предел прочности.

Для обеспечения надежности и долговечности эти опасные напряжения снижают до некоторой величины, т.е. их величина ограничивается так называемыми допускаемыми напряжениями.

В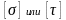 еличина допускаемых напряжений устанавливается для каждого материала на основе опыта, путем расчета.

О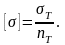 бозначают напряжение его символом:

Допускаемое напряжение для пластичных материалов

(например, углеродистая сталь):

Д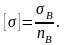 опускаемое напряжение для хрупких материалов

(например, чугун):

Критерии прочности и разрушения материалов.

Критерии прочности конструкций и их отдельных элементов

основаны на особенностях сопротивления материалов действующим нагрузкам и условиях перехода материала к предельному состоянию.

Критерии прочности являются основой при разработке так называемых теорий прочности.

Критерии не учитывают наличие в материале дефектов

Критерии прочности конструкций и их отдельных элементов основаны на особенностях сопротивления материалов действующим нагрузкам и условиях перехода материала к предельному состоянию.

Критерии прочности являются основой при разработке так называемых теорий прочности.

Критерии не учитывают наличие в материале дефектов.

3. Центральное растяжение сжатие. Определение нормальных напряжений в поперечном сечении. Продольные и поперечные деформации стержня. Закон Гука, упругие постоянные материала. Условие прочности.

-----------------------------------------------------------------------------------------------------------------------------------

Растяжением или сжатием называют вид нагружения бруса, в поперечном сечении которого возникает только продольная сила N.

Иногда говорят – центральное (простое или осевое) растяжение.

В реальных конструкциях кроме продольной силы в сечениях бруса действуют и другие силовые факторы.

Растяжение (сжатие) встречается:

– в различных элементах строительных конструкций (мачты, колонны, опоры, трубы, стержни ферм);

– в элементах механизмов и машин (шток поршня, трос) и т.д.

Рассмотрим стержень постоянного поперечного сечения А, к концам которого вдоль его оси приложены равные и противоположно направленные силы F.

В произвольном сечении возникает продольная сила

N = F.

П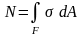 окажем произвольное поперечное сечение стержня. В этом сечении выделим элементарную площадку dA.

Продольная сила в сечении площадью А определяется интегралом

Анализ показывает, что на достаточном удалении от мест приложения внешней силы (гипотеза Сен-Венана) сечения после нагружения остаются плоскими, а только перемещаются параллельно самим себе (гипотеза Бернулли – плоских сечений).

Следовательно, по всему сечению действуют нормальные напряжения одинаковой величины: σ=const.

Н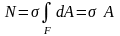 ормальная сила равна

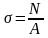
откуда

Продольные и поперечные деформации

Под действием продольной силы стержень изменяет свою длину – деформируется (удлиняется или укорачивается).

Абсолютная линейная деформация Δℓ – приращение длины стержня.

Рассмотрим участок стержня элементарной длины dz.

Видим, что после приложения нагрузки – продольной силы

данный участок получит абсолютную линейную деформацию Δdz.

З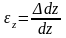 наем, что относительная продольная деформация определяется отношением

С учетом принципа Сен-Венана и выводов о том, что нормальные напряжения при растяжении-сжатии постоянны следует постоянство продольной деформации по высоте и ширине сечения ε = const – справедлива гипотеза плоских сечений.

Суммируя абсолютные удлинения малых элементов Δdz = εdz по всей длине стержня, получим:

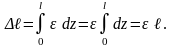
[м, см, мм]

М,см,мм

Суммируя абсолютные удлинения малых элементов Δdz = εdz по всей длине стержня, получим:

Относительная продольная деформация

с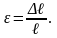 тержня при простом растяжении: измеряется в %

Легко видеть, что и в направлении осей X и Y поперечное сечение стержня также деформируется – поперечные размеры сечения уменьшаются при его растяжении и увеличиваются при сжатии.

Это есть поперечная деформация:

абсолютная: Δh, Δb;

о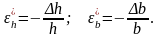 тносительная:

Они записаны со знаком минус, т.к. продольная и поперечная деформации имеют обратные знаки.

О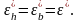 тметим, что для изотропных материалов

Упругие постоянные материала

Опытами установлено, что отношение относительной поперечной к относительной продольной деформации для каждого материала есть величина постоянная.

Это отношение, взятое по абсолютной величине называется коэффициентом поперечной деформации

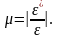( коэффициентом Пуассона):

Коэффициент Пуассона µ (мю) – всегда положительная и безразмерная величина. В теории упругости обозначают ν (ню).

Определяется опытным путем для каждого материала и условий испытаний и не может быть больше 0,5.

Эту величину впервые теоретически получил француз Пуассон: он считал, что для всех материалов – 0,25.

В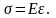 упругой стадии работы для большинства конструкционных материалов напряжения и деформации (например, при растяжении) связаны прямой пропорциональной зависимостью (участок ОА диаграммы):

К оэффициент пропорциональности

Е – модуль продольной упругости

(модуль упругости при растяжении или модуль упругости I рода или модуль Юнга).

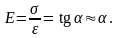
Из диаграммы и формулы следует, что модуль Е определяется углом наклона α прямой на участке ОА

Модуль упругости I рода есть упругая постоянная материала и характеризует способность материала сопротивляться упругим деформациям растяжения или сжатия.

Определяется опытным путем – испытанием образца, изготовленного из исследуемого материала.

Имеет размерность напряжений (Па).

Закон Гука

Установлен опытным путем:

при растяжении стержня силой F он получит абсолютную деформацию Δℓ.

При пропорциональном увеличении силы в такой же пропорции увеличится и деформация.

Закон Гука описывается формулой, справедливой в пределах упругих деформаций материала:

Нормальные напряжения прямо пропорциональны относительным линейным деформациям.

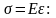
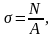
Известно, что а После подстановки в формулу закона Гука

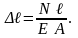
Данная формула – еще одна форма записи закона Гука.

Абсолютное удлинение или укорочение стержня Δℓ прямо пропорционально нормальной силе N и первоначальной длине стержня ℓ и обратно пропорционально площади поперечного сечения A и модулю продольной упругости E.

Расчет на прочность

Применим метод расчета по допускаемым напряжениям.

И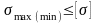 сходя из него, условие прочности может быть записано (соответственно для нормальных или касательных напряжений) в виде:

Для проведения расчета необходимо:

– определить вид нагружения (путем построения эпюр внутренних силовых факторов);

– на основании анализа эпюр определить опасное сечение бруса (сечение, в котором приложен экстремальный по величине внутренний силовой фактор);

– для выявленного вида нагружения и для его опасного сечения записать условие прочности (в одних случаях – по нормальным напряжениям, в других – по касательным, а при сложных видах нагружения условие прочности имеет более сложный вид).

Условие прочности при растяжении-сжатии записывается в виде:

– для бруса постоянного сечения (F=const):

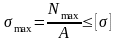
– для бруса ступенчатого сечения

(размеры или форма сечения изменяются):

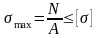
– для бруса материал которого неодинаково сопротивляется растяжению и сжатию

(материал имеет разные значения допускаемых напряжение при растяжении и сжатии):