13.Рост трещин при циклическом нагружении. Формула Париса.

____________________________________________________________________________________

Рост трещин при циклическом нагружении

10.6.1 Эмпирическая формула Париса

Как оценить долговечность, т.е. число циклов нагружения на стадии роста трещины (при увеличении длины трещины от начального L₀ до критического L_с значения)?

Для чего?

Оценка долговечности важна при расчете ресурса изделий.

Долговечность материала по числу циклов N на стадии роста трещин:

число циклов при увеличении длины трещины от начального ее значения до критического,

оценивается различными зависимостями.

Наиболее распространена эмпирическая формула П. Париса.

Ф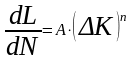 ормула Париса основана на том, что все явления на кончике трещины, в том числе и скорость ее распространения зависят от КИН.

dL/dN – скорость роста трещины;

А, n – эмпирические коэффициенты

ΔK = (K_max – K_min) – перепад коэффициента интенсивности напряжений за один цикл нагружения.

Показатель n для разных материалов располагается в интервале от 2 до 7 (чаще всего n =4 ).

Чем больше n, тем более хрупкое состояние материала наблюдается при испытании.

Многочисленные экспериментальные исследования хорошо подтверждают эту формулу.

Б олее удобна запись формулы Париса в виде:

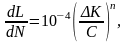
С – эмпирический коэффициент

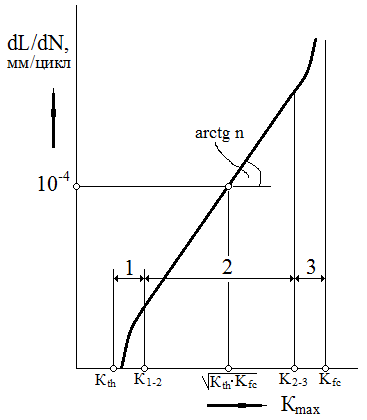
Формулы описывают средний (линейный) участок полной диаграммы усталостного разрушения, которая в большинстве случаев имеет S-образный вид.

К_th – пороговый КИН (англ. threshold– порог),

K_fc – вязкость разрушения при доломе (полном разрушении): англ. fatigue – долом.

1 и 3 – области низких и высоких скоростей роста трещины

2 – область справедливости формулы Париса

При наложении воздействия активной среды форма диаграммы будет изменяться.

В процессе циклического нагружения механические свойства материала изменяются (даже вдалеке от вершины трещины), поэтому K_fС < К_IС.

Из многих механических факторов, влияющих на скорость роста усталостной трещины, наибольшая роль принадлежит коэффициенту асимметрии цикла r.

Известно, что при постоянном значении ∆К величина dL/dN растет с ростом r, причем тем в большей степени, чем в более хрупком состоянии находится материал

(и чем меньше ∆К).

Приведенные формулы Париса (существует несколько вариантов записи) применяются как для малоцикловой, так и многоцикловой усталости.

Специалисты в области механики разрушения рекомендуют следующий порядок расчета на долговечность по числу циклов в связи с ростом трещин.

1 Выявить на основе количественной оценки возможностей дефектоскопического контроля максимальную длину (глубину) начальной трещины, существующей в элементе конструкции и подобрать наиболее подходящее выражение (формулу) для определения коэффициента интенсивности напряжений К.

2 По вязкости разрушения К_С или К_IC (в зависимости от предполагаемой степени стеснения деформации вдоль фронта трещины) и номинального эксплуатационного (расчетного) напряжения σ_max в сечении трещины найти по критерию Ирвина критическую длину трещины L_C.

3 Рассчитать параметры цикла ∆К = К_max ‒ К_min и r = σ_min / σ_max по известным напряжениям цикла σ_max и σ_min.

4 Экспериментально получить соотношение для циклической скорости роста трещины dL/dN в функции параметров задачи, которая представляется одной из зависимостей (формулой) Париса.

Вид функции и значения постоянных материала определяются при лабораторных испытаниях на усталость с регистрацией кривых роста трещины (L – N) в образцах, для которых известно решение для КИН.

5 Решить задачу прогнозирования роста усталостной трещины.