
- •1.Реальная конструкция и ее расчетная схема. Основные гипотезы о деформируемом теле. Метод сечений. Типы нагружения бруса. Напряжения, перемещения и деформации.
- •2. Метод расчета конструкций по допускаемым напряжениям. Критерии прочности и разрушения материалов.
- •3. Центральное растяжение сжатие. Определение нормальных напряжений в поперечном сечении. Продольные и поперечные деформации стержня. Закон Гука, упругие постоянные материала. Условие прочности.
- •4.Прямой изгиб бруса. Зависимость между изгибающим моментом и кривизной оси прямого бруса.Формула Навье.Условие прочности.
- •5.Сдвиг.Определение касательных напряжений. Закон Гука. Определение перемещений. Условие прочности
- •6. Кручение стержня круглого поперечного сечения. Определение касательных напряжений.Определение перемещений.Условие прочности.
- •7. Структура и свойства конструкционных материалов. Влияние различных факторов на их свойства.
- •8. Диаграммы упругопластического деформирования конструкционных материалов
- •9.Анизотропия механических свойств материалов.
- •10. Ответ не найдет!
- •11. Напряжения на наклонных площадках и условия на поверхности.
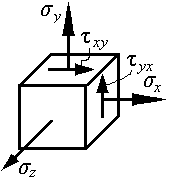
- •1 2. Тензор напряжений и его составляющие. Главные площадки и главные напряжения. Виды напряженных состояний.
- •13. Инварианты напряженного состояния. Интенсивность напряжений. Наибольшие касательные напряжения.
- •14.Выражение копмонентов деформаций через перемещения(состояние Коши)
- •16.Уравнения неразрывности (совместности) деформаций (уравнения Сен-Венана)
- •17.Обобщенный закон Гука
- •18.Работа упругих сил. Потенциальная энергия деформации.
- •1.Реологические модели материалов.
- •2.Теоритическая, техническая и конструкционная прочность.Пути повышения констр. Прочночсти.
- •3.Концентрация напряжений.
- •4. Модель тела с трещиной. Виды разрушения.
- •5.Влияние типа напряженно-деформированного состояния на разрушение. Хрупкое, квазихрупкое и вязкое разрушение упругого тела.
- •6. Энергетический подход к проблеме разрушения
- •7.Коэффициент при особенности напряжений.Формула Гриффитса.
- •8.Силовой и энергетический критерии механики разрушения.
- •10.Ивариантный j-интеграл.
- •11.Циклическая прочность материалов,механизм усталостного разрушения.Малоцикловая и многоцикловаяусталость материалов.
- •12 Влияние различных факторов на предел выносливости. Повышение выносливости конструктивными и технологическими мероприятиями.
- •13.Рост трещин при циклическом нагружении. Формула Париса.
- •14.Особенности коррозионного растрескивания и коррозионнго роста трещин в металлах.Коэффициент интенсивности напряжений.
- •15.Сопротивление разрушению элементов конструкций при высоких и низких температурах.
8.Силовой и энергетический критерии механики разрушения.
_____________________________________________________________________________________
Силовой критерий
П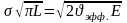 ереписав
формулу Ирвина-Орована, получим равенство,
аналогичное соотношениям, полученным
для формулы Гриффитса:
ереписав
формулу Ирвина-Орована, получим равенство,
аналогичное соотношениям, полученным
для формулы Гриффитса:
Коэффициент, имеющий обозначение K, получил название коэффициент интенсивности напряжений (КИН) или критерий Ирвина-Орована.
П о форме записи он аналогичен критерию Гриффитса. Имеет ту же размерность.
Условие Гриффитса и критерий Ирвина-Орована эквивалентны.
Однако критерий Ирвина-Орована более удобен в применении, т.к. в этом случае внимание сосредоточено на окрестности вершины трещины и можно оценивать опасность разрушения по интенсивности соответствующего напряженного состояния.
КИН (K) отражает геометрическую форму тела с трещиной и условия его нагружения.
Критический КИН ( KС ) есть характеристика материала – способность его сопротивляться раскрытию трещины, т.е. характеризует его трещиностойкость.
Критическое значение Kс, характеризует опасное физическое состояние тела (местные напряжения) в вершине трещины и зависит от расположения трещины и условий нагружения тела.
Глобальный энергетический критерий Гриффитса (рассматривается изменение энергии тела в целом) заменяется силовым в вершине трещины (рассматривается энергетическое состояние в вершине трещины).
Критический коэффициент интенсивности является силовым критерием разрушения, так как его можно трактовать как силу расширения трещины.
Критический КИН – трещиностойкость материала.
Вязкость разрушения - мера сопротивления росту трещины.
Трещиностойкость KC, имеет размерность коэффициента интенсивности напряжений [MПa м1/2].
Пластические деформации возникают в зонах высокой концентрации напряжений, в частности в вершине трещины.
В соответствии с упруго-пластическими моделями напряжения в вершине трещины являются конечной величиной.
Максимальные значения напряжений являются менее важной характеристикой по сравнению с коэффициентом интенсивности напряжений.
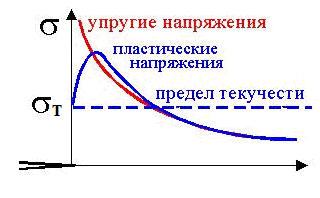
Пластические деформации возникают в зонах высокой концентрации напряжений.
Показаны особенности возникновения пластических деформаций в вершине трещины при уменьшении толщины пластины.
Формула Гриффитса для ПНС:
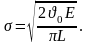
Ф
 ормула
Гриффитса для ПДС:
ормула
Гриффитса для ПДС:
Энергетический критерий
На основе анализа полей напряжений у вершины трещины Ирвин ввел понятие: скорость освобождения энергии или работы продвижения трещины на единицу длины.
В результате был сформулирован еще один критерий:
вязкость разрушения: G = 2эфф.
Обозначен буквой G в честь Гриффитса.
 Критическое
значение G
носит название энергетического критерия
механики квазихрупкого разрушения.
Критическое
значение G
носит название энергетического критерия
механики квазихрупкого разрушения.
Если G ≥ Gс, то трещина будет самопроизвольно развиваться.
Связь между силовым и энергетическим критериями имеет вид:
[Дж/м2]
[н∙м2/м
= н/м].
10.Ивариантный j-интеграл.
__________________________________________________________________________________
Для анализа вязких разрушений в нелинейной механике разрушения используются так называемые инвариантные интегралы, т.е. интегралы, не зависящие от контура интегрирования.
Наиболее широко используются: Г-интеграл (Г.П. Черепанов) и J-интеграл (Дж. Р. Райс).
Иногда они объединяются общим названием:
критерий J-интеграла (критерий Черепанова-Райса).
Это также энергетический критерий разрушения.
Он формулируется следующим образом:
трещина начинает распространяться, когда инвариантный J-интеграл достигает предельного значения JIc, т.е. J=JIc.
Потенциальная энергия деформации поступает к трещине через контур, охватывающий ее вершину, и затрачивается на разрушение.
Контур С охватывает вершину движущейся трещины.
Система координат x1, y1 неподвижна;
система координат x, y связана с вершиной трещины.
Баланс энергии вычисляется в движущейся системе координат x, y.
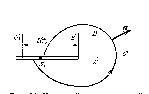
Обход контура С против хода часовой стрелки.
О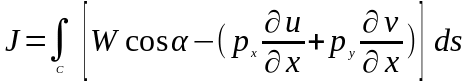 дин
из вариантов записи J –интеграла:
дин
из вариантов записи J –интеграла:
W - плотность энергии деформации;
px, py - вектора усилий, действующих на контур извне;
α - угол между нормалью n к контуру и осью x (линией трещины);
s - длина контура;
u, v - проекции полного перемещения вершины трещины на оси x, y.
J -интеграл не зависит от пути обхода трещины и определяется энергией, поступающей в зону у вершины трещины при увеличении трещины на единицу длины (изменение потенциальной энергии).
J
≤
JIc

Критерий разрушения в нелинейной механике разрушения:
