6. Энергетический подход к проблеме разрушения
__________________________________________________________________________________
Лист бумаги равномерно нагрузим вдоль продольной оси напряжениями. Лист останется целым.
В нагруженном листе выполним надрез (трещину).
Гриффитс рассмотрел эллиптический вырез в бесконечной пластине, подверженной растяжению и находящейся в условиях одноосного растяжения.
Материал принимался идеально хрупким и подчиняющимся закону Гука вплоть до разрушения: например, стекло.
Энергетически
замкнутая система с трещиной
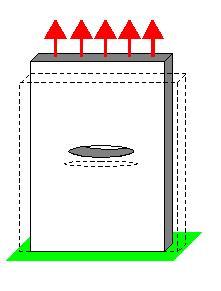
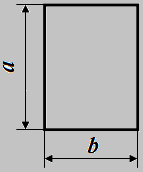
Размеры пластины (а, b) должны быть во много раз больше длины эллиптического выреза (большой полуоси эллипса длиной 2L).
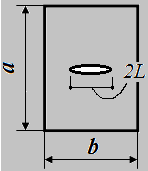
Для распространения (развития) трещины необходимо затратить энергию.
Так как система энергетически замкнута, то эта энергия может быть получена за счет уменьшения упругой энергии всей системы:
где-то внутри пластины должны уменьшиться напряжения.
Такая ситуация возможна, т.к. берега трещины под воздействием напряжений немного разойдутся, а это немедленно приведет к уменьшению напряжений вблизи её поверхности.
С некоторой степенью приближения: две треугольные области, затемненные на рисунке, отдадут энергию, т.е. при раскрытии трещины энергия освобождается.
Вершина трещины играет роль стока энергии, которая расходуется там же на образование новых поверхностей, т.е. в конечном счете на разрушение материала.
Одной только концентрации напряжений недостаточно для того, чтобы трещина росла.
Если не будет подвода энергии к вершине трещины, то она не сможет развиваться, т.е. разрушение не начнется или прекратится.
Энергетический баланс тела с трещиной
Условия развития трещины устанавливаются
уравнением энергетического баланса:
*величиной высвобождающейся вследствие продвижения трещины потенциальной энергии U (способствующей развитию трещины);
*величиной поверхностной энергии П, затрачиваемой на образование новых поверхностей (препятствующей развитию трещины).
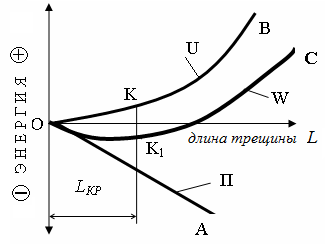
Гриффитс предположил, что трещина будет спонтанно (самопроизвольно) распространяться только тогда, когда общая энергия будет уменьшаться.
До точки К система в целом поглощает энергию.
После точки К энергия начинает выделяться из системы.
Существует некоторая критическая длина трещины (обозначаем Lкр).
Трещины, длина которых меньше Lкр, не могут самопроизвольно распространяться.
Т
рещины,
длина которых больше Lкр,
весьма опасны,
т.к. они могут расти сами по себе.
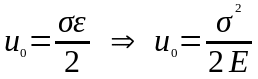
Потенциальная энергия
При одноосном напряженном состоянии удельная потенциальная энергия, запасенная в теле:
U
= u0
V
П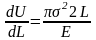
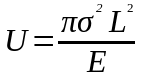ри
раскрытии трещины образуется эллиптическая
полость, для которой Гриффитс
ввел множитель :
7.Коэффициент при особенности напряжений.Формула Гриффитса.
__________________________________________________________________________________
Приравняем выражения производных от потенциальной энергии и от поверхностной энергии:
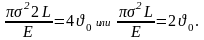
Получаем формулу Гриффитса:
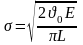
Коэффициент при особенности напряжений – глобальный энергетический критерий
Д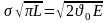
аже
при очень высоких локальных напряжениях
на концах трещин конструкция безопасна
и не разрушается до тех пор, пока в теле
нет трещины, длина которой превышает
ее критическую длину.
Перепишем формулу Гриффитса в виде равенства:
Д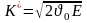
ля
каждого материала К/
есть величина постоянная.
[н/м3/2]
[Па√м] [нм1/2/м2].
Гриффитс назвал КI коэффициентом при особенности напряжений.
При его определении рассматривалось изменение энергии тела в целом, поэтому коэффициент КI носит также название
глобального энергетического критерия.
КI характеризует способность весьма хрупких материалов (например, стекла) противостоять росту трещин.
Доказательства Гриффитса о существовании коэффициента КI
Опыты на стеклянных колбах.
В них выполнялись трещины разной длины, затем колбы отжигались для снятия остаточных напряжений и подвергались действию внутреннего гидравлического давления до разрушения. При этом измерялось напряжение разрушения.
Оказалось, что в этих опытах
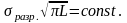Если в процессе
нагружения элемента напряжение возрастает
до величины разрушающего напряжения,
то его называют критическим и обозначают
кр.