1.Реологические модели материалов.
Отдельные идеальные материалы (тела или модели) в реологии носят имена выдающихся ученых.
Все реологические модели имеют механические аналоги, с помощью которых изучаются свойства этих тел.
В механике изучаются два идеальных тела, которые с двух сторон ограничивают классические тела реологии.
Абсолютно твердое тело – тело Евклида (материал под нагрузкой не деформируется, т.е. = 0). Эта модель является предметом изучения в теоретической механике.
Идеальная жидкость – тело Паскаля (касательные компоненты напряжений равны нулю: = 0, т.е. равны нулю силы вязкого взаимодействия частей жидкости). Тела с такими свойствами изучаются в гидравлике.
Идеальное линейно–упругое тело – тело Гука. Эта модель является предметом изучения в теории упругости и сопротивлении материалов.
диаграмма
деформирования
механический
аналог
Вязкая жидкость – тело Ньютона или Ньютонова жидкость. Изучается в гидродинамике.
Идеальное жесткопластическое тело – тело Сен-Венана.
Предмет изучения в теории идеальной пластичности.
Поведение материала моделируется элементом сухого трения.
Идеальное упругопластическое тело – тело Прандтля.
Характеризуется наличием линейной упругости до достижения предела текучести и пластическим течением – после достижении этого предела.
Поведение материала моделируется комбинацией пружины и элемента сухого трения (тел Гука и Сен-Венана).
Наиболее часто используемая модель материала.
Общим для тел Сен-Венана и Прандтля является то, что процесс накопления пластической деформации не ведет к повышению напряжений в теле.
Различным образом компонуя идеальные тела можно составить модель с определенными реологическими свойствами, например:
линейно упрочняющееся тело без площадки текучести – два тела Гука с разными упругими свойствами
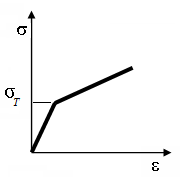
линейно упрочняющееся тело с площадкой текучести – два тела Гука в сочетании с телом Прандтля.
В приложении к телу с растущей трещиной использование изложенных подходов, состоит из следующих действий:
а) выбор реологической модели материала;
б) описание разрушения (процесс разрушения в разных материалах и при разных условиях протекает по-разному);
в) построение критерия разрушения.
2.Теоритическая, техническая и конструкционная прочность.Пути повышения констр. Прочночсти.
Теоретическая (идеальная) прочность
Это прочность идеальных монокристаллов, вычисленная через силы межатомного взаимодействия.
Физика твердого тела и квантовая механика позволяют количественно оценить теоретическую прочность любого материала, если известно его строение и химический состав, однако экспериментальное определение теоретической прочности весьма сложно.
Прочность при растяжении идеального кристаллического тела –напряжение, необходимое для разрушения тела по определенной кристаллографической плоскости.
Условно это напряжение можно подсчитать путем деления силы, необходимой для разрушения, на единичную площадь пространства между атомами.
Силу, необходимую для разрушения, принимают равной силе связи изолированной пары атомов.
Теоретическое разрушающее напряжение, в случае идеального кристаллического тела, для большинства материалов оказывается равным:
п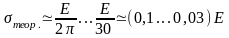
ри
растяжении (сжатии)
п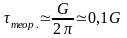
ри
сдвиге (срезе)
Т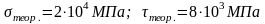
огда
для стали Ст.3:
Техническая (реальная) прочность
Это прочность, достигаемая в реальных материалах.
Реальная прочность оценивается напряжением, характеризующим прочность самого материала.
Определяется экспериментально, например, испытанием образцов на растяжение.
Реальная прочность кристаллических и стекловидных тел меньше теоретической прочности примерно на два порядка.
Для пластичных материалов она характеризуется их пределом прочности (например, для стали Ст.3 – при растяжении В=400 МПа, при срезе В=250 МПа).
Акад. А.Ф. Иоффе (в 1920 г. на примере эксперимента с кристаллом каменной соли):
экспериментально измеренная прочность кристаллов составляет несколько десятков единиц МПа. После снятия некоторого поверхностного слоя (путем опускания в горячую воду) прочность кристалла достигла значения около 2000 МПа (что только в 2 раза меньше теоретической прочности кристалла).
Вывод – вместе с поверхностным слоем были удалены трещины и другие дефекты.
Таким образом, чем более совершенна структура кристалла, тем ближе значение прочности материала к теоретической:
Конструкционная прочность
Прочность элементов конструкции или конструкции в целом – прочность их в заданных условиях эксплуатации (нагружения).
Прочность конструкции в целом определяется разрушающей нагрузкой Fраз. [Н], которая приводит к разрушению конструкции.
Выбор характеристик для оценки конструкционной прочности материала зависит от характера нагружения и вида нарушения прочности данной конструкции.
Это понятие применимо только к конкретной конструкции.