1 Реологические модели материалов.

Реология – совокупность методов исследования течения и деформации реальных сред.

Одна из основных задач реологии – установление связей между параметрами, характеризующими физические признаки тела (материала), проявляемые в микроопыте.

Отдельные идеальные материалы (тела или модели) в реологии носят имена выдающихся ученых.

Все реологические модели имеют механические аналоги, с помощью которых изучаются свойства этих тел.

Абсолютно твердое тело – тело Евклида (материал под нагрузкой не деформируется, т.е. = 0). Эта модель является предметом изучения в теоретической механике.

Идеальная жидкость – тело Паскаля (касательные компоненты напряжений равны нулю:  = 0, т.е. равны нулю силы вязкого взаимодействия частей жидкости). Тела с такими свойствами изучаются в гидравлике.

Идеальное линейно–упругое тело – тело Гука. Эта модель является предметом изучения в теории упругости и сопротивлении материалов.

Поведение материала моделируется пружиной, т. е. механическим аналогом является пружина. Материал обладает идеальной упругостью во всем диапазоне деформирования.

Вязкая жидкость – тело Ньютона или Ньютонова жидкость. Изучается в гидродинамике.

Идеальное жесткопластическое тело – тело Сен-Венана.

Предмет изучения в теории идеальной пластичности.

Поведение материала моделируется элементом сухого трения.

Идеальное упругопластическое тело – тело Прандтля.

Характеризуется наличием линейной упругости до достижения предела текучести и пластическим течением – после достижении этого предела.

Поведение материала моделируется комбинацией пружины и элемента сухого трения (тел Гука и Сен-Венана).

Наиболее часто используемая модель материала.

В приложении к телу с растущей трещиной использование изложенных подходов, состоит из следующих действий:

а) выбор реологической модели материала;

б) описание разрушения (процесс разрушения в разных материалах и при разных условиях протекает по-разному);

в) построение критерия разрушения.

2 Теоретическая, техническая и конструкционная прочность. Пути повышения конструкционной прочности.

Теоретическая (идеальная) прочность

Это прочность идеальных монокристаллов, вычисленная через силы межатомного взаимодействия.

Прочность при растяжении идеального кристаллического тела –напряжение, необходимое для разрушения тела по определенной кристаллографической плоскости.

Условно это напряжение можно подсчитать путем деления силы, необходимой для разрушения, на единичную площадь пространства между атомами.

Силу, необходимую для разрушения, принимают равной силе связи изолированной пары атомов.

при растяжении (сжатии)

при сдвиге (срезе)

Техническая (реальная) прочность

Это прочность, достигаемая в реальных материалах.

Реальная прочность оценивается напряжением, характеризующим прочность самого материала.

Определяется экспериментально, например, испытанием образцов на растяжение.

Реальная прочность кристаллических и стекловидных тел меньше теоретической прочности примерно на два порядка.

чЕМ более совершенна структура кристалла, тем ближе значение прочности материала к теоретической.

Конструкционная прочность

Прочность элементов конструкции или конструкции в целом – прочность их в заданных условиях эксплуатации (нагружения).

Прочность конструкции в целом определяется разрушающей нагрузкой F_раз. [Н], которая приводит к разрушению конструкции.

Выбор характеристик для оценки конструкционной прочности материала зависит от характера нагружения и вида нарушения прочности данной конструкции.

Это понятие применимо только к конкретной конструкции.

3 Концентрация напряжений.

Явление резкого увеличения напряжений вблизи особенностей поверхности называется концентрацией напряжений, а сами особенности поверхности – концентраторами напряжений.

распределение напряжений в стержне без концентратора

то же с концентратором

_к – напряжение в вершине концентратора

_о – номинальное напряжение

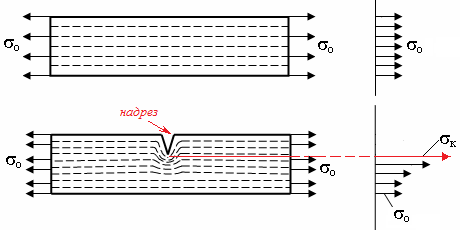
Концентраторы напряжений значительно повышают локальные (местные) напряжения, что иногда приводит к аварийным разрушениям конструкций при их эксплуатации:

разрушения мостов, корпусов кораблей и самолетов;

котлов, трубопроводов, атомных реакторов и т.д.

Очень важна при этом температура эксплуатации, особенно, если она низкая.

Надрез: является концентратором напряжений как при растяжении, так и при сжатии.

Трещина: при сжатии берега ее смыкаются.

Она передает сжимающие напряжения как сплошной материал.

4 Модель тела с трещиной. Виды разрушения.

5 Влияние типа напряженно-деформированного состояния на разрушение. Хрупкое, квазихрупкое и вязкое разрушение упругого тела.

С позиций механики разрушение описывается в рамках строго сформулированных и достаточно общих моделей.

Использование основных положений, законов и методов механики сплошной среды и определило название науки – механика разрушения.

Под разрушением понимают исчерпание несущей способности конструкции, произошедшее вследствие наступления беспрепятственного пластического течения (за счет необратимых остаточных деформаций) или из-за накопления повреждений.

Начальное разрушение – образование и развитие пор, трещин и других нарушений сплошности (дефектов), распределенных по всему объему материала, которые понижают его прочностные свойства.

Полное разрушение – разделение тела на части.

В зависимости от величины пластической деформации разрушение: пластическое, хрупкое и квазихрупкое.

Пластическое разрушение

(вязкое или идеально-пластическое)

Происходит после существенной пластической деформации и является результатом исчерпания несущей способности (способности материала сопротивляться пластическим деформациям).

Особенностью идеально-пластического разрушения является то, что во всех элементах конструкции эквивалентные напряжения достигают предела текучести.

Во всей зоне разрушения  = _Т.

Хрупкое разрушение (упругое)

Происходит без пластических деформаций (например, при испытаниях на ударную вязкость).

После разрушения тело можно составить заново.

При этом виде разрушения нестабильный рост трещины происходит при напряжениях, меньших предела текучести.

Напряжения в зоне разрушения  < _Т.

Хрупкое разрушение зачастую может развиваться с большой скоростью, вследствие чего оно представляет наибольшую опасность.

Особенности:

■ наличие концентраторов напряжений;

■ невозможность релаксации напряжений в момент начала роста образовавшейся трещины, т.е. действующие нагрузки и особенности НДС не позволяют напряжениям релаксировать в материале;

■ толщина сечения элементов конструкций. Как правило, хрупко разрушаются конструкции, имеющие сечения большей толщины. Однако хрупко могут разрушаться и конструкции с очень тонкими сечениями из стали и алюминиевых сплавов при действии переменных напряжений;

Квазихрупкое разрушение

При исследованиях изломов выявляется некоторая зона пластической деформации перед фронтом трещины и пластически деформированный (наклепанный) металл у ее поверхности, хотя картина разрушения такая же, как и для хрупкого материала.

Пластичность и хрупкость не являются постоянными свойствами материала.

Большинство металлических материалов может разрушаться и пластично, и хрупко, в зависимости от температуры, скорости нагружения, концентрации напряжений и т.д.

Трещины.

В механике разрушения изучается несущая способность нагруженного тела с трещиной и процесс его разрушения.

Трещина в своем развитии проходит

три стадии:

зарождение, рост и распространение.

При этом она может находиться в одном из двух состояний:

– устойчивом (равновесном). Это значит, что при квазистатическом (условно статическом) увеличении нагрузки трещина переходит из одного устойчивого состояния в другое;

– неустойчивом (неравновесном). При малейшем увеличении нагрузки начинается очень быстрое развитие трещины вплоть до полного разрушения тела.

Схематическое представление трещины в теле

традиционно в виде эллипса

Влияние типа напряженно-деформированного состояния (НДС)

При нагружении тела в материале возникают упругие деформации, которые с увеличением нагрузки переходят в пластические.

Плоское напряженное состояние:

все действующие на материальную точку напряжения параллельны одной плоскости.

Закон Гука для ПНС:

Н апример, в тонких пластинках и оболочках

Плоское деформированное состояние:

все точки тела перемещаются параллельно одной плоскости.

Например, в длинных призматических телах под действием поперечных сил, в толстых пластинах (плитах).

В направлении толщины тела (в направлении оси Z) полностью отсутствуют как упругие, так и пластические деформации (ε_z=0).

Пунктирная линия – исходный размер

6 Энергетический подход при анализе процесса разрушения.

Гриффитс рассмотрел эллиптический вырез в бесконечной пластине, подверженной растяжению и находящейся в условиях одноосного растяжения.

Материал принимался идеально хрупким и подчиняющимся закону Гука вплоть до разрушения: например, стекло.

В первые с энергетической точки зрения процесс разрушения рассмотрел английский инженер Гриффитс

Энергетически замкнутая система с трещиной - Размеры пластины (а, b) должны быть во много раз больше длины эллиптического выреза (большой полуоси эллипса длиной 2L).

Для распространения (развития) трещины необходимо затратить энергию.

Так как система энергетически замкнута, то эта энергия может быть получена за счет уменьшения упругой энергии всей системы:

где-то внутри пластины должны уменьшиться напряжения.

Такая ситуация возможна, т.к. берега трещины под воздействием напряжений немного разойдутся, а это немедленно приведет к уменьшению напряжений вблизи её поверхности.

Вершина трещины играет роль стока энергии, которая расходуется там же на образование новых поверхностей, т.е. в конечном счете на разрушение материала.

Одной только концентрации напряжений недостаточно для того, чтобы трещина росла.

Если не будет подвода энергии к вершине трещины, то она не сможет развиваться, т.е. разрушение не начнется или прекратится.

7 Коэффициент при особенности напряжений. Формула Гриффитса.

Коэффициент при особенности напряжений – глобальный энергетический критерий

Даже при очень высоких локальных напряжениях на концах трещин конструкция безопасна и не разрушается до тех пор, пока в теле нет трещины, длина которой превышает ее критическую длину.

Перепишем формулу Гриффитса в виде равенства:

Для каждого материала К^/ есть величина постоянная. (Произведение после знака равно)

Гриффитс назвал К^I коэффициентом при особенности напряжений.

При его определении рассматривалось изменение энергии тела в целом, поэтому коэффициент К^I носит также название глобального энергетического критерия.

К^I характеризует способность весьма хрупких материалов (например, стекла) противостоять росту трещин.

_{эфф. – поверхностная плотность} энергии или плотность поверхностной энергии. Лень смотреть.

8 Силовой и энергетический критерии механики разрушения.

Силовой критерий

Переписав формулу Ирвина-Орована, получим равенство, аналогичное соотношениям, полученным для формулы Гриффитса:

Коэффициент, имеющий обозначение K (СПРАВА ПОСЛЕ РАВНО), получил название коэффициент интенсивности напряжений (КИН) или критерий Ирвина-Орована.

По форме записи он аналогичен критерию Гриффитса. Имеет ту же размерность.

Условие Гриффитса и критерий Ирвина-Орована эквивалентны.

Однако критерий Ирвина-Орована более удобен в применении, т.к. в этом случае внимание сосредоточено на окрестности вершины трещины и можно оценивать опасность разрушения по интенсивности соответствующего напряженного состояния.

Критический КИН ( K_С ) есть характеристика материала – способность его сопротивляться раскрытию трещины, т.е. характеризует его трещиностойкость.

Энергетический критерий

На основе анализа полей напряжений у вершины трещины Ирвин ввел понятие: скорость освобождения энергии или работы продвижения трещины на единицу длины.

В результате был сформулирован еще один критерий:

вязкость разрушения: G = 2_эфф.

Обозначен буквой G в честь Гриффитса.

Критическое значение G носит название энергетического критерия механики квазихрупкого разрушения.

Если G ≥ G_с, то трещина будет самопроизвольно развиваться.

Связь между силовым и энергетическим критериями имеет вид:

[Дж/м²]

[н∙м²/м = н/м].

9 Виды деформаций в вершине трещины. Деформационные критерии механики разрушения.

Основные типы деформаций в зоне трещины

1. Т рещины нормального отрыва

(раскрытия трещины)

тип деформации I.

Берега трещины перемещаются в направлении оси Y

2. трещины поперечного симметричного сдвига (плоская деформация) – тип деформацииII. Берега трещины перемещаются в направлении оси X

3. трещины несимметричного (продольного) сдвига (антиплоская деформация) – тип деформации III. Берега трещины перемещаются в направлении оси Z.

Деформационные критерии

Образование зоны пластических деформаций вблизи трещины приводит к увеличению ее длины по сравнению со случаем упругих деформаций.

Следовательно, при решении квазихрупкой задачи следует учитывать эффективную длину трещины L_эфф., которой определяется протяженность зоны пластического деформирования вблизи вершины трещины

1)Протяженность пластической зоны в теле с трещиной

По значениям коэффициента интенсивности и предела текучести материала оценивается протяженность пластической зоны.

2)Критическое раскрытие трещины

Имеются различные модели образования пластической зоны в вершине трещины, которые позволяют заменить трещину с пластической зоной на трещину с чисто упругой зоной.

10 Инвариантный J-интеграл.

Для анализа вязких разрушений в нелинейной механике разрушения используются так называемые инвариантные интегралы, т.е. интегралы, не зависящие от контура интегрирования.

Наиболее широко используются: Г-интеграл (Г.П. Черепанов) и J-интеграл (Дж. Р. Райс).

Иногда они объединяются общим названием:

критерий J-интеграла (критерий Черепанова-Райса).

трещина начинает распространяться, когда инвариантный J-интеграл достигает предельного значения J_Ic, т.е. J=J_Ic.

J -интеграл не зависит от пути обхода трещины и определяется энергией, поступающей в зону у вершины трещины при увеличении трещины на единицу длины (изменение потенциальной энергии).

Предельное (критическое) значение J_Ic, называемое упругопластической вязкостью разрушения, определяется экспериментально по кривым нагрузка - перемещение для образца с трещиной.

Критерий разрушения в нелинейной механике разрушения:

J ≤ J_Ic

11 Циклическая прочность материалов, механизм усталостного разрушения. Малоцикловая и многоцикловая усталость материалов.

Общие понятия и определения циклического нагружения

Разрушение материалов под действием переменных во времени нагрузок наблюдается ПРИ РАБОЧИХ НАГРУЗКАХ (напряжениях), ВЕЛИЧИНА КОТОРЫХ НАМНОГО МЕНЬШЕ в сравнении с их допускаемыми значениямиПоэтому явление разрушения под действием переменных во времени нагрузок изучают специалисты различных отраслей.

ЦИКЛ НАГРУЗОК (НАПРЯЖЕНИЙ) N – есть совокупность всех последовательных значений переменных нагрузок (напряжений) за один период процесса их изменения.

ПЕРИОД ЦИКЛА Т – есть промежуток времени между двумя последующими максимальными (или минимальными) значениями нагрузок (напряжений).

Для многоцикловой усталости характерна очень малая величина рабочих напряжений:

Малоцикловая усталость чаще всего наблюдается при рабочих напряжениях, близких по величине пределу текучести материала.

Объясняются эти особенности значительной неоднородностью структуры, анизотропией механических свойств, наличием дефектов, историей и условиями нагружения и эксплуатации, конструктивными особенностями и технологией изготовления и т.п.

12 Влияние различных факторов на предел выносливости. Повышение выносливости конструктивными и технологическими мероприятиями.

ПРЕДЕЛ ВЫНОСЛИВОСТИ (предел усталости) – максимальное напряжение, при котором материал способен сопротивляться нагружению не разрушаясь, при любом произвольно большом числе циклов нагружений.

ВЫНОСЛИВОСТЬ – способность материалов и конструкций сопротивляться разрушению при их повторно-переменных нагружениях.

Различают МАЛОЦИКЛОВУЮ усталость (разрушение наступает при малом числе циклов нагружения) и МНОГОЦИКЛОВУЮ усталость (разрушение наступает при большом числе циклов нагружения).

Усталостная прочность материалов и конструкций (предел выносливости) в значительной степени и существенно зависит от целого ряда факторов:

конструктивных особенностей и технологии изготовления деталей и конструкций (отверстия, сварные швы, дефекты и т.п.)

Они объединяются термином –

концентрация напряжений;

абсолютных размеров деталей;

состояния и качества обработки поверхности деталей;

особенностей окружающей среды;

особенностей нагружения, в частности паузы (перерывы в нагружении);

температуры эксплуатации и ряда других факторов.

Повышение выносливости конструктивными и технологическими мероприятиями

Конструктивные мероприятия

При проектировании деталей, узлов и конструкций конструктор должен стремиться в первую очередь к снижению влияния концентрации напряжений:

Рекомендации сводятся к обеспечению плавных очертаний переходов к сечениям других размеров, выемок, подрезов, переходов от катетов швов к основному металлу, оптимизации размеров (радиуса) галтелей: переход по радиусу.

Большая жесткость детали также приводит к снижению усталостной прочности. Поэтому необходимо, по возможности снижать жесткость, на этом основана идея разгружающих надрезов и так называемых «выкружек».

В процессе проектирования необходимо также учитывать и влияние масштабного фактора – оптимизация размеров деталей и всей конструкции

Технологические мероприятия

– снижение концентрации напряжений при обработке; – повышение качества обработки поверхностей (снижение ); – обеспечение получения материалов без дефектов или с минимальным их присутствием; – оптимизацию процессов химико-термической обработки; – проектирование и выполнение сварочных и сборочных операций с целью снижения вероятности появления дефектов, концентрации напряжений, а также снижения уровня остаточных напряжений.

Рекомендации сводятся к обеспечению качества обработки поверхностей (лучше всего шлифование или полирование), упрочнению (наклеп с применением методов ППД), химико-термическая обработка (азотирование, электрохимические покрытия при работе в коррозионной среде). Особо следует отметить необходимость учета свойств применяемого материала

13 Рост трещин при циклическом нагружении. Формула Париса.

Эмпирическая формула Париса

Оценка долговечности важна при расчете ресурса изделий

Долговечность материала по числу циклов N на стадии роста трещин:

число циклов при увеличении длины трещины от начального ее значения до критического, оценивается различными зависимостями.

Формула Париса основана на том, что все явления на кончике трещины, в том числе и скорость ее распространения зависят от КИН.

dL/dN – скорость роста трещины;

А, n – эмпирические коэффициенты

ΔK = (K_max – K_min) – перепад коэффициента интенсивности напряжений за один цикл нагружения.

Многочисленные экспериментальные исследования хорошо подтверждают эту формулу.

Более удобна запись формулы Париса в виде:

мм/цикл

Более удобна запись формулы Париса в виде:

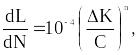
14 Особенности коррозионного растрескивания и коррозионного роста трещин в металлах. Коэффициент интенсивности напряжений.

Коррозионные среды оказывают сильное влияние и на циклическую трещиностойкость конструкционных материалов. Это в первую очередь проявляется в ускорении распространения трещин.

Различают три основных механизма влияния коррозионных сред на трещиностойкость конструкционных материалов:

водородное охрупчивание;

адсорбционное понижение прочности;

локальное анодное растворение.

По влиянию на характер разрушения активные среды можно разделить на:

1) среды, вызывающие охрупчивание металла и его хрупкое разрушение в напряженном состоянии (например, водородное охрупчивание, а также коррозионное растрескивание в электролитах и жидких металлах);

2) среды нейтральные;

3) среды, способные пластифицировать металл.

Под действием среды (1) и эксплуатационных условий может изменяться также критический размер трещин, что приводит к существенному уменьшению долговечности.

Коррозионное растрескивание: квазихрупкое разрушение с малой величиной пластической деформации в вершине трещины и малой скоростью развития коррозионной трещины по сравнению с механическим лавинным разрушением.

Специфика роста коррозионных трещин проявляется в их ветвлении и затуплении (за счет анодного растворения металла в их вершине), а также в различии параметров среды в вершине трещины и на поверхности образцов.

Ветвление: микро- (межзеренный рост трещин) и макро- (проявляется в наличии нескольких равноценных, одновременно распространяющихся ветвей на расстоянии большем, чем величина зерна).

Коэффициент интенсивности напряжений

Для характеристики прочности материала в агрессивной среде введен коэффициент

К_scc (scc – stress corrosion cracking – коррозионное растрескивание) – критический коэффициент интенсивности напряжений при коррозионном растрескивании.

Его величина постоянна для данного материала и определенной среды.

К_scc не зависит от геометрии образца, но чувствителен к внешним условиям и свойствам материала.

Установлено, что при наличии неблагоприятной среды (например, морской воды) в условиях постоянного нагружения можно определить некоторое пороговое значения К_scc, ниже которого роста трещины в данной коррозионной среде не наблюдается.

Пороговое значение К_scc определяет начало интенсивного влияния среды на развитие трещины и ускорение ее роста.

Вместе с тем, по К_scc можно определить ту минимальную нагрузку и тот минимальный дефект, ниже которых разрушение не имеет места в данной среде:

15 Сопротивление разрушению элементов конструкций при высоких и низких температурах

Температурные напряжения могут вызвать пластическую деформацию и разрушение, представляют существенную опасность для хрупких материалов и являются важным фактором при оценке прочности элементов конструкций.

Вследствие изменения температуры меняются механические характеристики материала и вид диаграммы растяжения.

При неоднородном распределении температур (температура точек элемента различна) неоднородными становятся и свойства материала.

На схеме показаны характерные температурные области работы конструкций.

Кратковременное действие нагрузки

1 – гладкий образец

2 – образец с острым концентратором

Длительное действие нагрузки

3 – гладкий образец

4 – образец с надрезом, медленное нагружение