
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
- •Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
- •1. Вычислите: a) , б) , в) , г) .
- •2. Решите уравнение: a) , б) ,
- •3. Вычислите площадь фигуры, изображенной на рисунке.
- •7. Решите неравенство: a) , б) ,
Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
Вариант 1.
1. Вычислите:
a)  ,
б)
,
б)  , в)
, в) 
 , г)
, г) 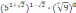 .
.
2. Решите
уравнение: a)  ,
б)
,
б)  ,
,
в) 5 7
sin x
2
cos2 x
= 0, г)
7
sin x
2
cos2 x
= 0, г)  .
.
3. Вычислите площадь фигуры, изображенной на рисунке:
а)
 б)
б)

4. Материальная
точка движется прямолинейно
по закону x(t)
 (где x — расстояние от
точки отсчета в метрах, t —
время в секундах, измеренное
с начала движения). Найдите
ее скорость (в м/с) в момент
времени t = 4 с.
(где x — расстояние от
точки отсчета в метрах, t —
время в секундах, измеренное
с начала движения). Найдите
ее скорость (в м/с) в момент
времени t = 4 с.
5. Для
получения на экране
увеличенного изображения
лампочки в лаборатории
используется собирающая
линза с главным фокусным
расстоянием f
= 30см. Расстояние от линзы до
лампочки - 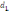 ,
а расстояние
,
а расстояние  от линзы до экрана равно 180 см.
Изображение на экране будет
четким, если выполнено
соотношение
от линзы до экрана равно 180 см.
Изображение на экране будет
четким, если выполнено
соотношение  .
Укажите, на каком расстоянии
от линзы можно поместить лампочку,
чтобы еe изображение на экране
было чeтким. Ответ выразите в
см.
.
Укажите, на каком расстоянии
от линзы можно поместить лампочку,
чтобы еe изображение на экране
было чeтким. Ответ выразите в
см.
6. Найдите наибольшее значение функции:
a)
y = 12cos x
+ 6 на отрезке
на отрезке 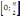 ,
б) y =
,
б) y =  на отрезке
на отрезке 
 .
.
7. Решите
неравенство: a)  ,
б)
,
б)  ,
,
в) 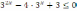 ,
г)
,
г)  .
.
8. а) На рисунке
изображен график функции y
= f(x) и ее
касательная к нему в точке с абсциссой
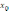 .
Найдите значение производной функции
f(x) в точке
(рис.а).
.
Найдите значение производной функции
f(x) в точке
(рис.а).
б) На рисунке
изображен график производной
функции f(x),определенной
на интервале
 .
Найдите: промежутки
возрастания и убывания функции
f(x), укажите
их длины; количество точек экстремума;
точки, в которых f
‘(x)=0; точки «max»;
точки «min» (рис. б).
.
Найдите: промежутки
возрастания и убывания функции
f(x), укажите
их длины; количество точек экстремума;
точки, в которых f
‘(x)=0; точки «max»;
точки «min» (рис. б).
а)
 б)
б)
Экзаменационная работа для проведения государственного выпускного экзамена по математике (первый курс)
Вариант 2.
1. Вычислите: a) , б) , в) , г) .
2. Решите уравнение: a) , б) ,
в) 8 cos2
x
12
sin x + 7 = 0,
г) 
3. Вычислите площадь фигуры, изображенной на рисунке.
а ) б)
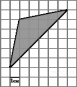

4. Материальная
точка движется прямолинейно
по закону x(t)
 (где x — расстояние от
точки отсчета в метрах, t —
время в секундах, измеренное
с начала движения). Найдите
ее скорость (в м/с) в момент
времени t = 3 с.
(где x — расстояние от
точки отсчета в метрах, t —
время в секундах, измеренное
с начала движения). Найдите
ее скорость (в м/с) в момент
времени t = 3 с.
5. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 50см. Расстояние от линзы до лампочки - , а расстояние от линзы до экрана равно 150 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в см.
6. Найдите наименьшее значение функции:
a)
y = 8sin x
 4
4 на отрезке
на отрезке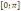 ,
б) y =
,
б) y = 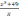 на отрезке
на отрезке  .
.
7. Решите неравенство: a) , б) ,
в)  ,
г)
,
г) 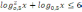 .
.
8. а) На рисунке изображен график функции y = f(x) и ее касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке (рис.а).
б) На рисунке изображен график производной функции f(x),определенной на интервале . Найдите: промежутки возрастания и убывания функции f(x), укажите их длины; количество точек экстремума; точки, в которых f ‘(x)=0; точки «max»; точки «min» (рис.б).
а)
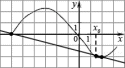 б)
б)
