14.Таблица основных интегралов Основные формулы

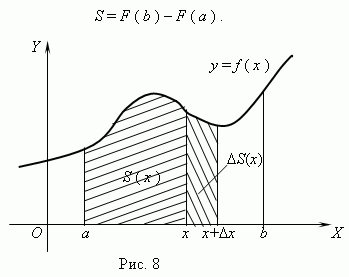
15.криволинейная трапеция,формула Ньютона-Лейбница Рассмотрим непрерывную функцию  y = f ( x ), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак ( рис.8 ).  Фигура, ограниченная графиком этой функции, отрезком [ a, b ] и прямыми  x = a и x = b, называется криволинейной трапецией.  Для вычисления площадей криволинейных трапеций используется следующая теорема:

 Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b], т.e.

Рассмотрим функцию S ( x ), заданную на отрезке [ a, b ]. Если a<x   b, то S ( x ) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку ( x, 0 ). Отметим, что если   x = a ,  то  S ( a ) = 0, а  S ( b ) = S  ( S – площадь всей криволинейной трапеции). Можно доказать, что

                       

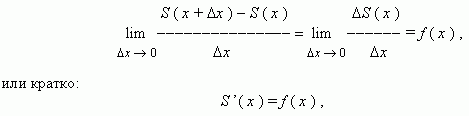
т.e. S ( x ) – первообразная для  f ( x ). Отсюда, согласно основному свойству первообразных, для всех  x  [ a, b ]  имеем:

 S ( x ) = F ( x ) + C ,

 

где C – некоторая постоянная,  F – одна из первообразных функции  f .

Чтобы найти C , подставим  x = a :

 F ( a ) + C = S ( a ) = 0,

 

отсюда, C = F ( a ) и  S ( x ) = F ( x ) F ( a ). Так как площадь криволинейной трапеции равна  S ( b ) , то подставляя  x = b , получим:

 S = S ( b ) = F ( b ) F ( a ).

 

П р и м е р .  Найти площадь фигуры, ограниченной кривой  y = x² и прямыми

                       y = 0,  x = 1,  x = 2  ( рис.9 ) .

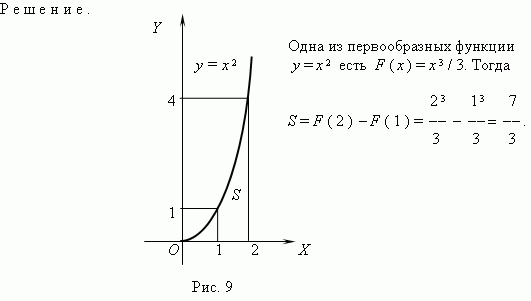
Формула Ньютона - Лейбница. Сравнивая две формулы для площади криволинейной трапеции, приходим к следующему заключению: если F ( x ) - первообразная функции f ( x ) на отрезке [ a, b ], то

 

Это и есть знаменитая формула Ньютона – Лейбница. Она справедлива для любой функции  f ( x ), непрерывной на отрезке  [ a, b ] .

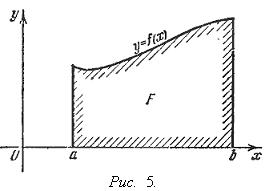
16.геометрический смысл определенного интеграла Если f(x) непрерывна и положительна на [a, b], то интеграл

представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) 

17.формулы вычесления объема тела вращения Пусть   — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми   и   и графиком непрерывной функции  .

Докажем, что это тело вращения кубируемо и его объем выражается формулой

Сначала докажем, что это тело вращения регулярно, если в качестве   выберем плоскость  , перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии   от плоскости  , является кругом радиуса   и его площадь   равна   (рис. 46). Поэтому функция  непрерывна в силу непрерывности  . Далее, если  , то это значит, что  . Но проекциями сечений на плоскость   являются круги радиусов   и   с центром  , и из   вытекает, что круг радиуса   содержится в круге радиуса  .

Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле

Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми    , то

Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.

В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.

Например, найдем объем тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой y#, в основании которого лежит отрезок  . Этот объем равен разности объемов двух прямых круговых цилиндров

Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:

Отсюда легко следует формула объёма тела вращения вокруг оси ординат:

18. аксиомы стереометрии и их следствия Основные фигуры в пространстве: точки, прямые и плоскости.

рис. 1	рис. 2	рис. 3

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

	А В        (точки А, В, С лежат в плоскости  ) С
рис. 4

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

	АB   Прямая АВ лежит в плоскости
рис. 5

Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

	а     = М Прямая а и плоскость   пересекаются в точке М.
рис. 6

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

	= a  и   пересекаются по прямой а.
рис. 7

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

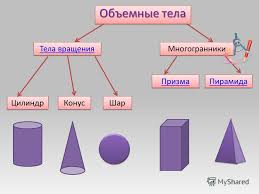
19.многогранник.Призма.параллелепипед.пирамида.конус .цилиндр.шар

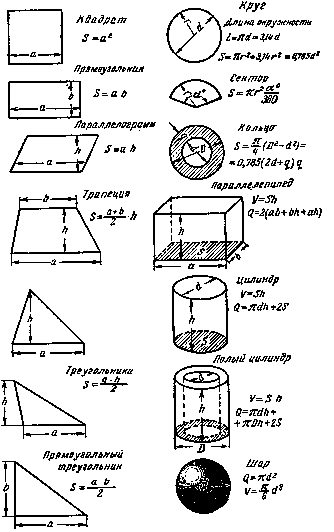
20.формулы площадей и объемов

21.формулы сокращенного умножения

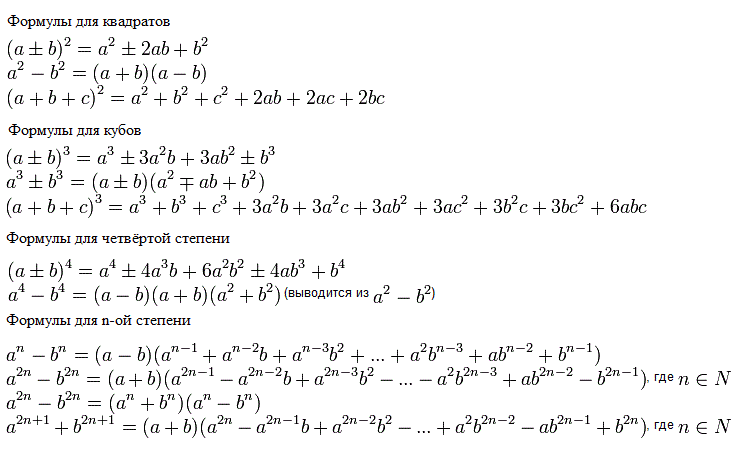
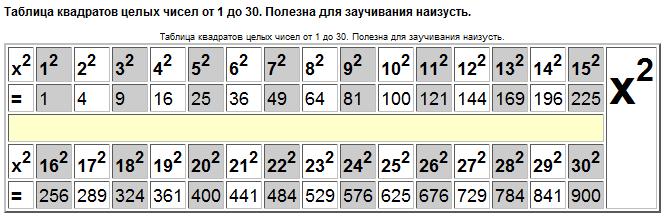
22.таблица квадратов 10-30

23.перестановки ,сочетания,размещения (формулы и определения) Размещения с повторениями

Определение. Отображение множества   первых натуральных чисел   в данное множество  , называется размещением с повторениями, составленным из данных   элементов по  .

Размещения с повторениями называются также конечными последовательностями.

Два размещения с повторениями одинаковы тогда и только тогда, когда на одинаковых местах находятся одни и те же элементы.

Если в размещении с повторениями некоторый элемент ставится в соответствие   различным натуральным числам, т.е., иначе говоря, данный элемент занимает   различных мест, то говорят, что этот элемент повторяется в размещении   раз.

Пример. Всевозможные размещения с повторениями из трех элементов   по 2:

Теорема. Число всевозможных размещений с повторениями из   элементов по   равно

Доказательство. По индукции. При   теорема верна, так как сами элементы   составляют всевозможные размещения элементов по одному, то число этих размещений равно  .

Предположим, что число размещений с повторениями из   элементов по   равно  . Составим из данных   элементов всевозможные размещения с повторениями по   элементу. Во всяком размещении с повторениями по   элементу

первые   элементов

образуют некоторое размещение с повторениями из   по   элементов. В качестве последнего  -го элемента   может быть взят любой из   элементов. При различных выборах   получаются различные размещения. Кроме того, два различные размещения  -го порядка дают два различные размещения  -го порядка.

Таким образом, число всех размещений  -го порядка равно

Задача. Имеется   различных книг, каждая в   экземплярах. Сколькими способами может быть сделан выбор книг из числа данных?

Перестановки с повторениями

Всякое размещение с повторениями, в котором элемент   повторяется   раз, элемент   повторяется   раз и т.д. элемент   повторяется   раз, где  ,  ,  ,   — данные числа, называется перестановкой с повторениями порядка

в которой данные элементы   повторяются соответственно  ,  ,   раз.

Теорема. Число различных перестановок с повторениями из элементов  , в которых элементы   повторяются соответственно   раз, равно

Доказательство. Если мы будем считать все   элементов перестановки с повторениями различными, то всего различных вариантов перестановок   элементов —  . Однако среди этих перестановок не все различны. В самом деле, все элементы   мы можем переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же, можем переставлять элементы  ,  ,  ,  . Таким образом, всякая перестановка может быть записана   способами. Следовательно, число различных перестановок с повторениями равно

Задача. Дано   различных предметов. Сколькими способами можно разбить эти предметы на 3 группы так, чтобы первая группа содержала   предметов, вторая   предметов, а третья   предметов?

Сочетания с повторениями

Определение. Если каждому элементу некоторого конечного множества поставлено в соответствие целое неотрицательное число — кратность данного элемента, то говорят, что задано сочетание с повторениями. Сумма   кратностей всех элементов называется порядком сочетания.

Всякое сочетание с повторениями  -го порядка, составленное из множества, содержащего   элементов, называется также сочетанием с повторением из   элементов по  .

Если   — кратности элементов  , то по определению   есть порядок сочетания

Теорема. Число сочетаний с повторениями из   элементов по   выражается формулой

Пример. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и картошка. Сколькими способами можно купить 7 пирожных?

Решение. Положим пирожные в коробку, а чтобы они не перепутались, разделим их картонными разделителями. Нужно 3 разделителя. Обозначения: 0 (картонки-разделители) и 1 — пирожные. Примерная покупка: 1110101101 — три наполеона, 1 эклер, 2 песочных и 1 картошка.

Итак два класса объектов 1 (7 штук) и 0 (3 штуки) — покупка — 10 объектов.

Два способа рассуждения:

(1) задача сводится к выбору мест для 7 пирожных (или для 3 разделителей) среди 10 объектов.

(2) другой способ рассуждения (эквивалентный). Надо разбить 10 мест на две группы: для 7 пирожных и 3 разделителей.

В чем особенность: объекты повторяются, причем один эклер на вкус неотличим от другого. Отсюда название: сочетания с повторениями. Можно представлять себе, что пирожные непрерывно пекут, так что они не переводятся, сколько ни ешь. Это совсем другая ситуация, чем в обычных сочетаниях!!!Пусть заданы два числа:   — число выбираемых элементов, и   — число типовэлементов, из которых производится выбор. Число    сочетаний с повторениями из элементов   типов равно числу способов выбора мест для собственно выбираемых элементов различных классов, или, что то же: для разделителей между ними.

Итак, основная формула:

Задача. Имеется   одинаковых предметов. Сколькими способами можно распределить этипредметы между   лицами?

Сочетания с повторениями с дополнительными условиями

Сколько существует сочетания с повторениями таких, что в них обязательно входят элементы   фиксированных типов?

Сразу возьмем по одному элементу указанного типа, и тогда уже сразу окажутся заняты   мест. Остальные   мест можно заполнять элементами прежних   типов.

В частности, пусть число типов   — числа выбранных элементов. Сколько существует сочетаний с повторениями, так что представлены хотя бы по одному все типы элементов?

Пример.   шаров размещаются по   ящикам. Сколько существует способов разместить их так, что пустых ящиков нет?Решение. Пусть нолики — шарики, а единички — стенки ящиков (потребуется   единичек). Две единички сразу кладем по краям.

Теперь положим между ними шарики-нолики, а далее нужно заполнить некоторые промежутки между ними так, чтобы между любыми двумя ноликами находилась не более одной единички. Значит, из   промежутков между шариками нужно выбрать места для   единичек. Всего таких способов  .

Метод координат. Подсчет числа путейРассмотрим координатную сетку: двигаясь по ней, помечаем каждый перекресток — производим суммирование числа возможных путей, ведущих на каждый перекресток. Получаем известный треугольник Паскаля.Поскольку на перекресток   на уровне   (считая сверху и принимая верхний уровень за нулевой) ведет   путей (число способов выбрать  движений направо вниз из общего числа   движений вниз), то свойство суммирования путей на перекрестке можно записать как

По прежнему остается справедливым свойство симметрии  .Формула включения — исключенияОпределение. Число элементов множества   называетсямощностью множества   иобозначается  .Теорема. Пусть даны множества  . Тогда количество элементов в объединении этих множеств можно найти по формуле:

Доказательство проводится по индукции. Пусть  . Нужно доказать формулу

Действительно, множество   состоит из всех элементов множества   и техэлементов множества  , которые не содержатся в множестве  . Тогда, сложив количества элементов во множествах   и  , мы двраза посчитаем количество элементов, общих для множеств   и  .Предположим, что формула включения — исключения справедлива для   множеств.Докажем ее для   множеств. Множество   можно представить в виде

Тогда получаем (первое равенство по формуле включения — исключения для двух множеств):

Используя формулу

и формулу включения — исключения для   множеств, получаем

В эту формулу  подставляем выражение, полученное ранее, и теорема доказана.