1. определите 2 и 3 порядка (правило треугольников)

Вычисление определителей второго порядка. Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу: Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной. Пример: .

Вычисление определителей третьего порядка. Определитель третьего порядка вычисляется по правилу: 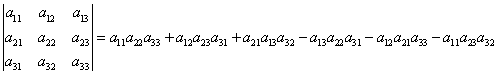Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников: 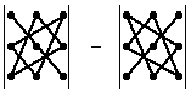Здесь схематично показано, какие сомножители соседствуют в слагаемых. Пример: Вычислить определитель: Решение: Воспользуемся правилом треугольников. Объясним картинку подробно, т.е. распишем каждое слагаемое отдельно:  

Итого:

2.числовая функция ,способы задания функции ,основные свойства функции.

Определение : Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.

Обозначение:

y = f(x),

где x – независимая переменная (аргумент), y – зависимая переменная (функция). Множество значений x называется областью определения функции (обозначается D(f)). Множество значений y называется областью значений функции (обозначается E(f)). Графиком функции называется множество точек плоскости с координатами (x, f(x))

Способы задания функции.

1. аналитический способ (с помощью математической формулы);

2. табличный способ (с помощью таблицы);

3. описательный способ (с помощью словесного описания);

4. графический способ (с помощью графика).

5. 1. Четность и нечетность

6. Функция называется четной, если       – область определения функции симметрична относительно нуля       – для любого х из области определения f(-x) = f(x)

Функция называется нечетной, если       – область определения функции симметрична относительно нуля       – для любого х из области определения f(-x) = –f(x)

График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом  , если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)< f(x₂).

4. Экстремумы

Точка Х_max называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Х_max , выполнено неравенство f(х)  f(X_max).

Значение Y_max=f(X_max) называется максимумом этой функции.

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

3.Замечательные пределы.

Замечательный тригонометрический предел Править

 (без доказательства)

Следствия

: 

Доказательство следствий

Замечательный показательно-степенной предел Править

 (без доказательства)

Следствия

Доказательство следствия

Замечательный логарифмический предел Править

Доказательство предела

• Используя замечательный показательно-степенной предел: 

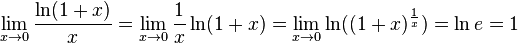
• Используя правило Лопиталя: 

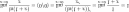
Замечательный показательный предел Править

Следствия

 для  , 

Доказательство предела

Доказательство следствия

Замечательный степенной предел Править

 (без доказательства)

См. также Править

4.свойства корней

1-е свойство корней Корень из произведения чисел равен произведение корней из этих чисел. `root n (a*b)=root n a *root n b` Например: `root 3 (8*27) = root 3 8 * root 3 27 = 2*3 = 6`

2-е свойство корней Корень из частного чисел равен частному корней из этих чисел. `root n(a/b) = root n a/ rootnb`, `b!=0` Например: `root 3 (1/27) = root 3 1 /root 3 27 = 1/3`

3-е свойство корней При извлечении корня из корня, степени корней перемножаются. `root n (root ma)=root (n*m) a` Например: `root 3 (root 4 5)= root (3*4) 5 = root 12 5`, `sqrt (root 3 7)=root(2*3) 7 =root 6 7`, `sqrt sqrt 16 = root (2*2) 16 = root 4 16 = 4`

4-е свойство корней Если число под знаком корня возвести в степень k, а показатель степени умножить на k, то первоначальное выражение не изменится. `root n a = root (n*k) (a^k)` Например: `root 3 27 = root (3*2) (27^2)=root 6 729`, и наоборот `root 6 81 = root (2*3) (9^2) = root 3 9`

5-е свойство корней Корень из числа возведенного в степень равен корню из этого числа возведенному в эту степень. `root n (a^k) = (root n a) ^k` Например: `sqrt (9^3) = (sqrt 9)^3=3^3=27`

6-е свойство корней Корень степени n из числа в степени n равен самому числу, если n нечетно, или модулю числа, если n четно. `root n (a^n) = a`, если `n` нечетно `root n (a^n) = |a|`, если `n` четно Например: ` root 5 (8^5) = 8`, `root 3 ((-7)^3) = -7`, `root 6 (35^6)=| 35|= 35`, `root 4 ((-5)^4) = |-5| = 5`

7-е свойство корней Чтобы внести число под знак корня нужно возвести его в степень корня. `b root n a = root n (a*b^n)` Например: `2 sqrt 3 = sqrt (3*2^2) = sqrt (3*4) = sqrt 12`, и, наоборот, `root 3 18 = root 3 (2*27) = root 3 (2* 3^3) = 3 root 3 2`

8-е свойство корней Если первое число меньше второго, то при извлечении корня одной и той же степени из обоих чисел, это неравенство сохраняется. Если `0<=a<=b`, то `root n a <= root n b` Например: `4<16` и `sqrt 4 < sqrt 16` `(2<4)`

5. иррациональные уравнения :определненное,способ решения.

Иррациональными называют уравнения в которых неизвестная величина находится под знаком корня определенного степени. Простейшие иррациональные уравнения решаются или подъемом в степень или заменой . Сложные иррациональные уравнения сводятся к предыдущим некоторыми искусственными методами . Например, такое на первый взгляд сложное уравнение

сводится к квадратному заменой

Зачастую при раскрытии иррациональности используют формулу сложного радикала

 1. Метод пристального взгляда

Уравнение с одной переменной   называют иррациональным, если хотя бы одна из функций   или   содержит переменную под знаком радикала. . Метод возведения обеих частей уравнений в одну и ту же степень.

Теорема.

Если возвести обе части уравнения   (1) в натуральную степень  , то уравнение  (2) является следствием уравнения (1).

Доказательство. Если выполняется числовое равенство  , то по свойствам степени выполняется равенство  , т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).

Если  , то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.

Если  , равенство   справедливо, если выполняется хотя бы одно из равенств   и  . Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения   приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование  . В этом случае уравнение   равносильно системе  . В системе отсутствует требование  , обеспечивающее существование корня степени  , т.к. оно было бы излишним в связи с равенством  .

Для реализации метода, основанного на этом утверждении требуется:

а) Выделить функцию, которая фигурирует в уравнении.

b) Записать область определения данной функции.

c) Доказать ее монотонность в области определения.

d) Угадать корень уравнения.

t) Обосновать, что других корней нет.

f) Записать ответ.

3. Решение уравнений с использованием замены переменной.

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

4. Метод разложения на множители выражений, входящих в уравнение.

Теорема.

Уравнение  , определенное на всей числовой оси, равносильно совокупности уравнений 

5. Метод выделения полных квадратов при решении иррациональных уравнений.

При решении некоторых иррациональных уравнений полезна формула 

6. Метод оценки.

Этот способ применим в том случае, когда подкоренные выражения представляют собой квадратный трехчлен, не раскладывающийся на линейные множители. Поэтому целесообразно оценить левую и правую части уравнения.

7. Иррациональные уравнения, содержащие степени выше второй.

Если уравнение имеет вид  то его можно решить , возводя обе части этого уравнения в степень  . Полученное уравнение   при нечетном  равносильно данному уравнению, а при четном  является нго следствием, аналогично рассмотренному выше случаю при 

6.Свойства лагорифмов

Специальные обозначения:

1. Натуральный логарифм  - логарифм по основанию  , где   - число Эйлера.

2. Десятичный логарифм 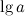  - логарифм по основанию 10.

Свойства логарифмов:

1°      - основное логарифмическое тождество.

2°    

3°    

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4°      - логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5°      - логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6°      - логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°    

8°    

9°      - переход к новому основанию.

7.Знаки тригонометрических функций по четвертям ,их четность-нечетность

Пусть при повороте около точки О на угол х начальный радиус   переходит в радиус   Из определений тригонометрических функций следует, что знак   совпадает со

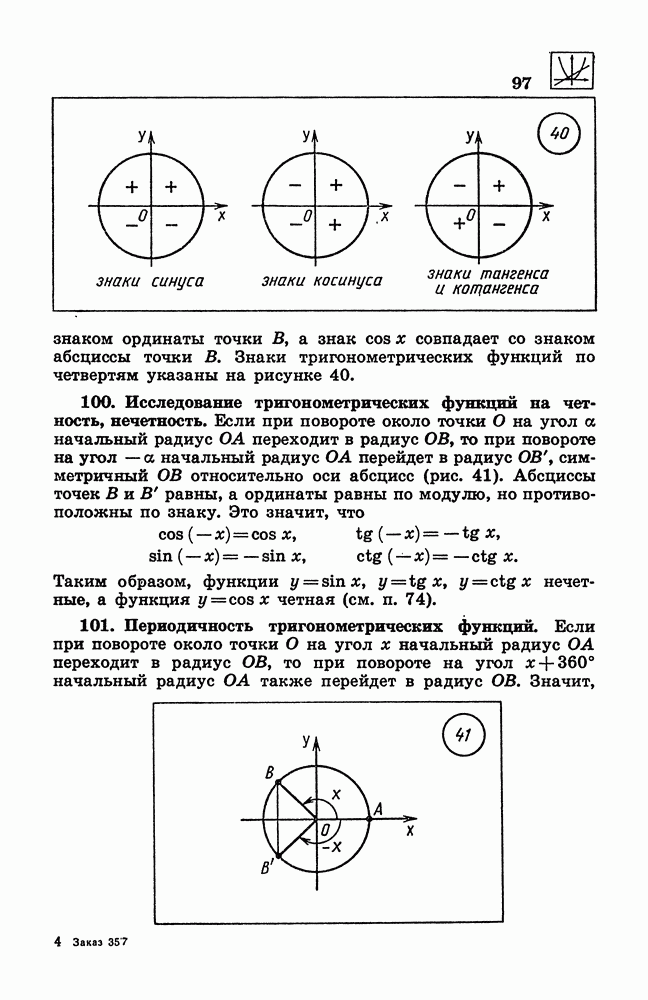
знаком ординаты точки В, а знак   совпадает со знаком абсциссы точки В. Знаки тригонометрических функций по четвертям

8.Основные тригонометрические тождества.Формулы суммы и разности ,сложения и вычитания.Формулы двойного и половинного аргумента. Основные тригонометрические тождества

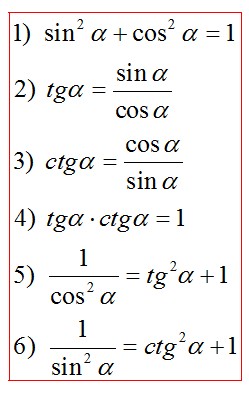
Формулы сложения и вычитания

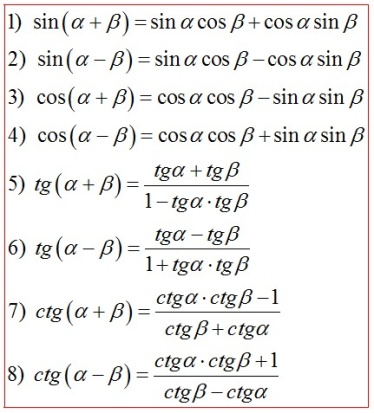
Формулы двойного угла

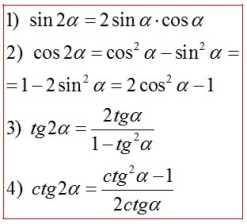
Формулы преобразования суммы и разности в произведение

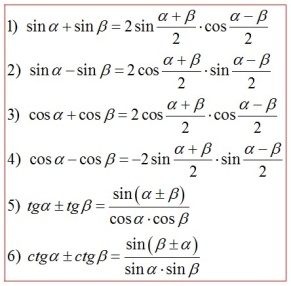
Формулы половинного аргумента

Формулы тройного угла*

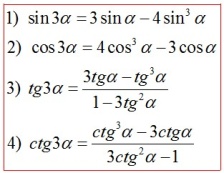
Формулы преобразования произведения в сумму (разность)*

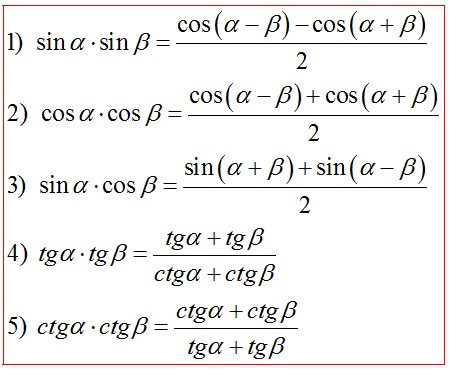
Универсальная подстановка через тангенс половинного аргумента*

9.график функций y=sinx.y=cosx Функция y = sin x

Графиком функции является синусоида.

Полную неповторяющуюся часть синусоиды называют волной синусоиды.

Половину волны синусоиды называют полуволной синусоиды (или аркой).   Свойства функции y = sin x:

1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это нечетная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика:     - с осью абсцисс: (πn; 0),     - с осью ординат: (0; 0). 6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках [2πn; π + 2πn] функция принимает положительные значения.      На промежутках [-π + 2πn; 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn].     Промежутки убывания функции: [π/2 + 2πn; 3π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn.     Точки максимума функции: π/2 + 2πn 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1,        наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π)

 

Для построения графика функции y = sin x удобно применять следующие масштабы:

- на листе в клетку за единицу отрезка примем длину в две клетки.

- на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.

- на оси y отметим 1, включающий две клетки.

 

Составим таблицу значений функции, применяя наши значения x:

x	0	π — 6	π — 3	π — 2	2π — 3	5π — 6	π
y	0	1 — 2	√3 — 2	1	√3 — 2	1 — 2	0

Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y= sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].

Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.

 

Функция y = cos x.

Графиком функции является синусоида (ее иногда называют косинусоидой).

 

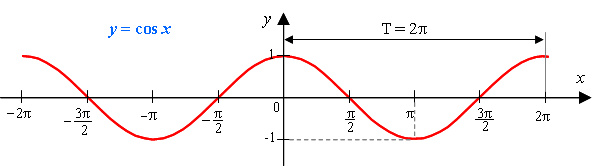
Свойства функции y = cos x:

1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика:     - с осью абсцисс: (π/2 + πn; 0),     - с осью ординат: (0;1). 6) На отрезке [0; π] функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения.     На промежутках [π/2 + 2πn; 3π/2 + 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn].     Промежутки убывания: [2πn; π + 2πn]; 9) Точки минимума функции: π + 2πn.     Точки максимума функции: 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1,        наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π)

 

Функция y = mf(x).

Возьмем предыдущую функцию y = cos x. Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m). Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.

Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.

Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.

 

Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.

 

Функция y = f(kx).

Если функция y = mf(x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y.

Причем k – любое действительное число.

При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.

 

10. геометрический и физический смысл производной Производной функции    в точке   называется предел отношения приращения функции в этой точке к приращению аргумента  ,  при  (если этот предел существует и конечен), т.е.

.

Обозначают: .

Производной функции   в точке  справа (слева) называется

(если этот предел существует и конечен).

Обозначают:    – производная y=f(x)  в точке справа,

  – производная y=f(x) в точке слева.