Оценка параметров

На основании результатов серии №1 из шести опытов удобно оценить четыре коэффициента в постулированной эмпирической формуле.

, (6.5)

пользуясь методом наименьших квадратов и свойствами скалярного произведения основных векторов.

Матрица независимых переменных x для серии №1 из шести опытов имеет вид.

Таблица 6.3

	X0	X1	X2	X3	№опыта	Т	y=lnT
						мин
X=	1	1	-1	-1	2	37	3,61
	1	-1	1	-1	3	165	5,11
	1	-1	-1	1	5	172	5,15
	1	1	1	1	8	18	2,89
	1	0	0	0	9	66	4,19
	1	0	0	0	10	83	4,42

Согласно методу наименьших квадратов необходимо, чтобы сумма квадратов отклонений фактических значений y от формальных, полученных по уравнению (6.3) была наименьшей, т.е.

. (6.6)

Левую часть выражения (7.6) обозначим буквой f (f-функция от неизвестных параметров , , , ).

Минимум этой функции найдем из уравнений

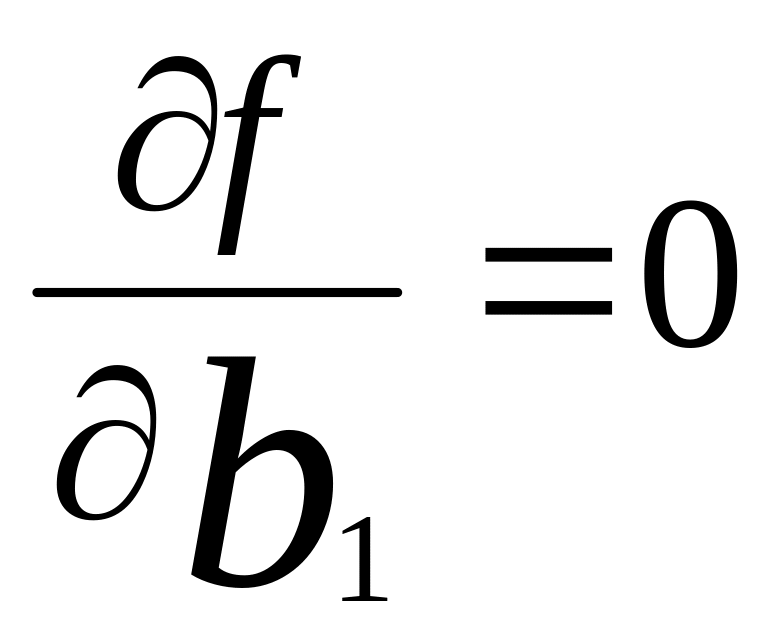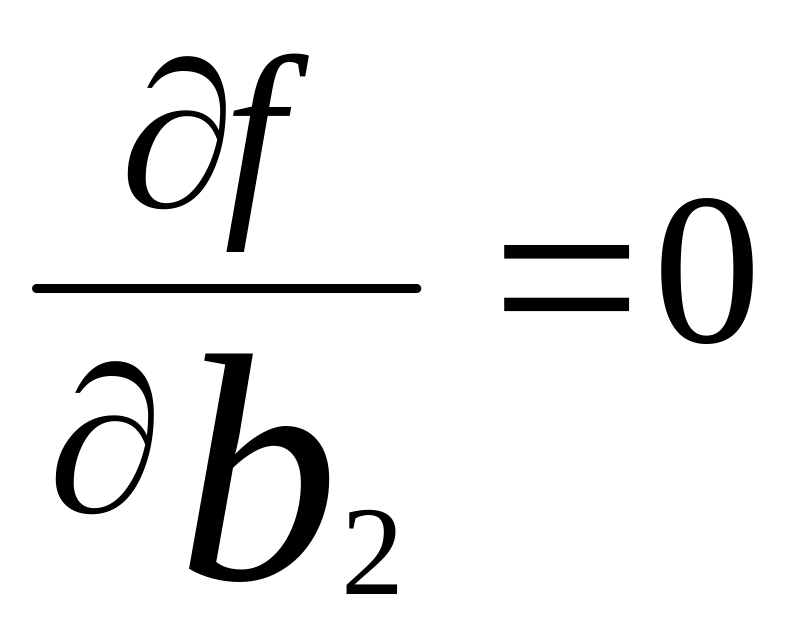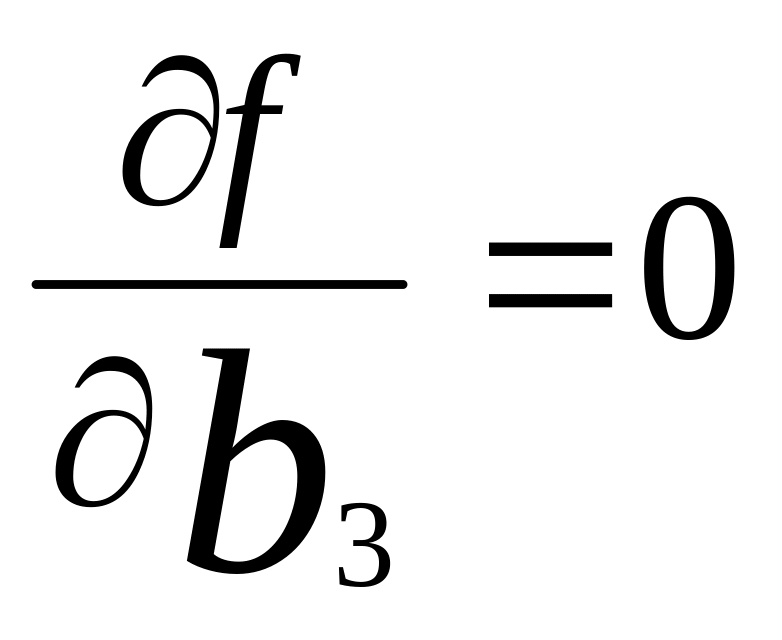; ; ; . (6.7)

Продифференцировав, напишем систему этих уравнений в окончательном виде:

(6.8)

Уравнения (7.8) дают возможность определить где – n число опытов; в нашем примере n=6.

; ;

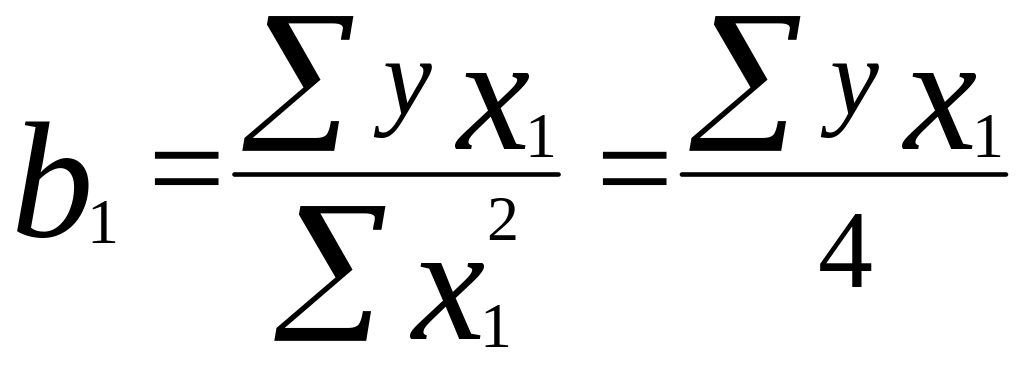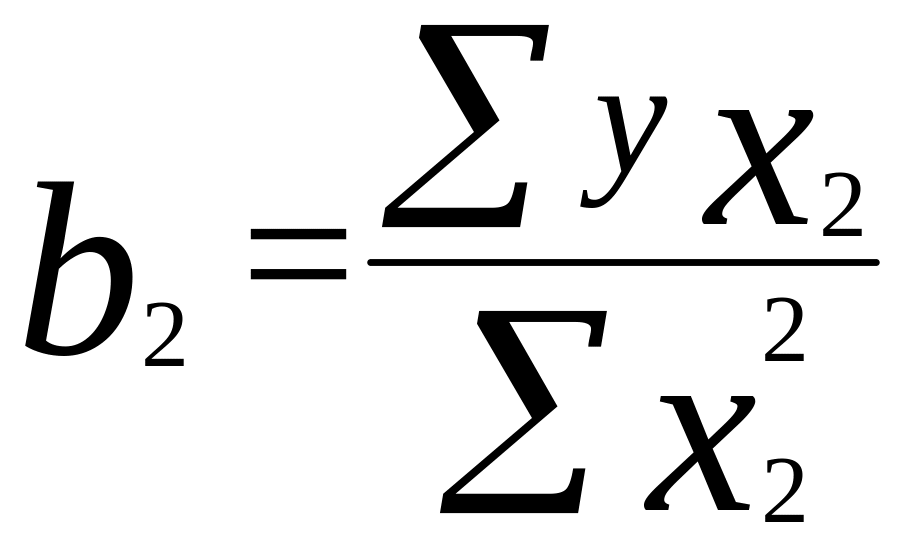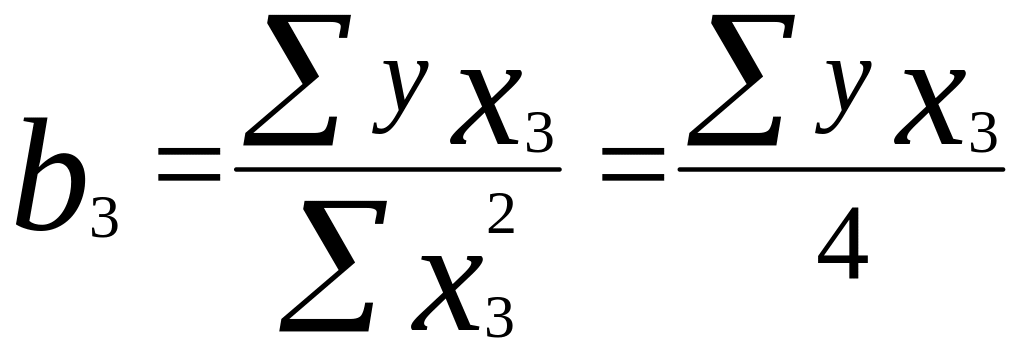
(6.9)

Необходимо добавить, что другие члены уравнений будут равны нулю в силу ортогональности векторов , , и

Очевидно: было бы проще не решать уравнения (6.6) (6.8), а воспользоваться матрицами и .

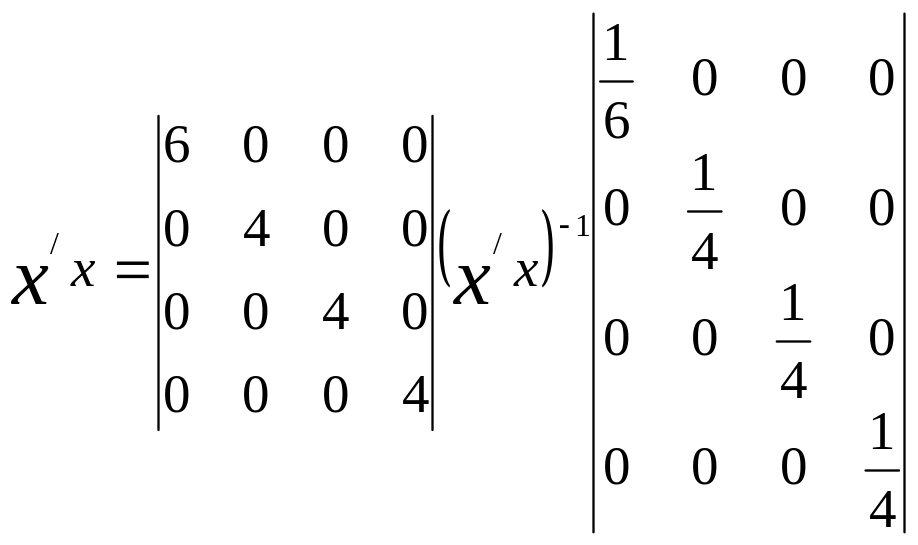
Согласно уравнениям (6.9), имеем:

Здесь индексы при y обозначают номера опытов (таблица 6.2)

Подставив в последние уравнения опытные значения из серии №1, можно получить формулу для стойкости резца:

(6.10)

Формулу (6.10) необходимо расшифровать, согласно уравнениям (6.4):

Подставляя значения , , в уравнение (6.10), получим

Следовательно

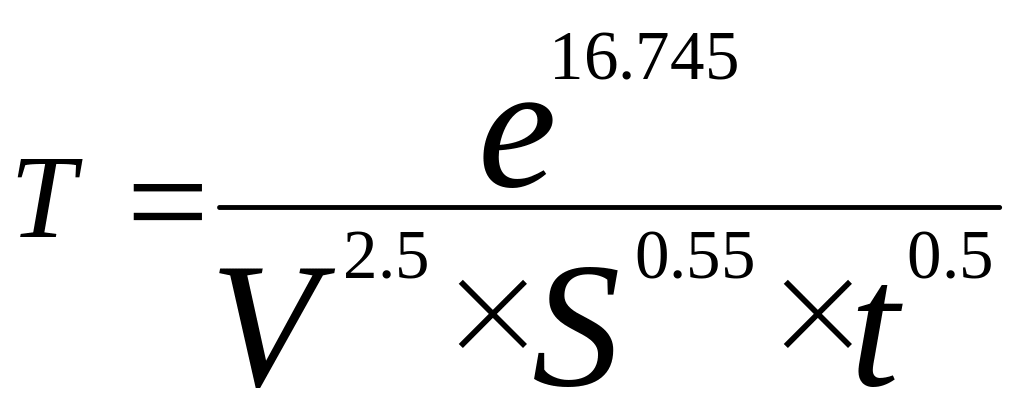мин (6.11)

После статистического анализа результатов серии №1 опытов, когда выявились слишком большие интервалы колебаний стойкости при 95% достоверности, были выполнены еще шесть опытов серии №2 исследований. В результате всех опытов получена формула:

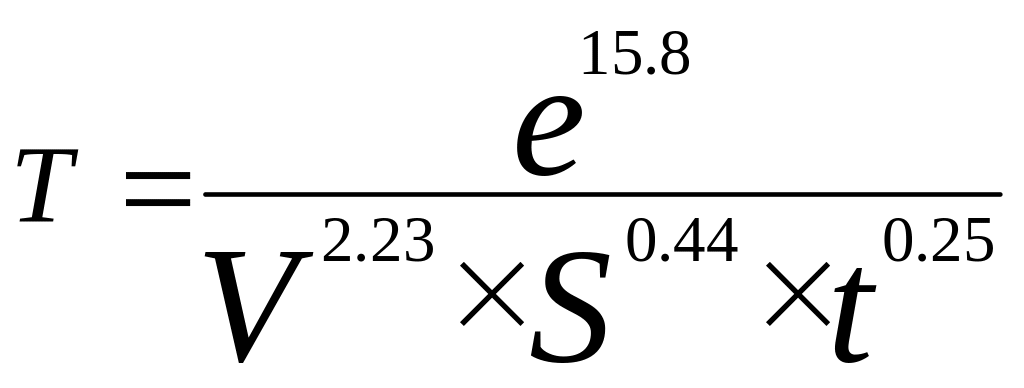мин , (6.12)

Формула мало отличается от формулы (6.11), но 95%-ные доверительные интервалы значительно улучшились, благодаря большему числу опытов.

Упрощенный вывод зависимостей

(на примере составляющей силы резания)

Г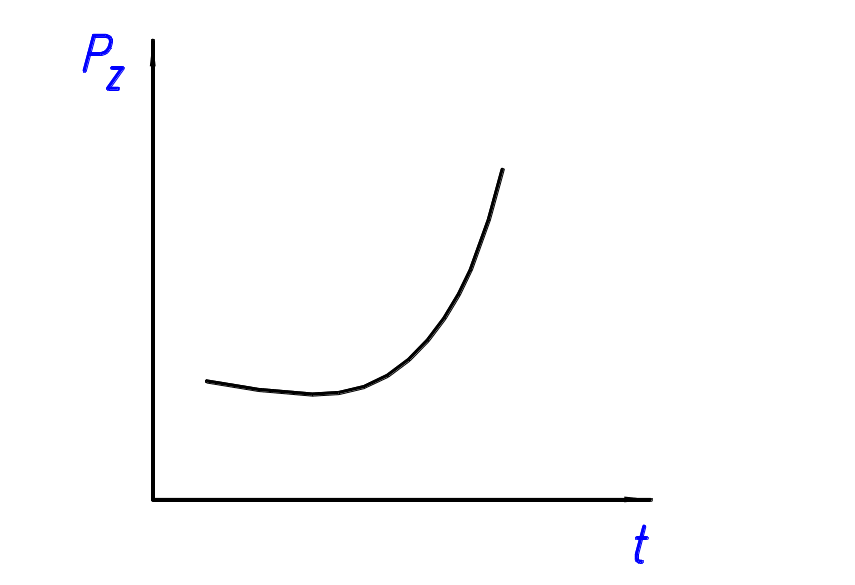 рафик зависимости главной составляющей силы резания от глубины резания описывается параболической зависимостью (рис. 6.2).

Рис. 6.2. График зависимости от

Для вывода уравнения зависимости показателей построение графиков выполним в двойных логарифмических координатах. При этом график зависимости показателей выразится прямой линией.

Рассмотрим пример для комбинации, где S и V постоянные, а t – переменная. В этом случае зависимость:

имеет вид (6.13)

Прологарифмировав уравнение (6.13), получим следующее уравнение:

Обозначим ; ; ;

Получим следующее уравнение:

(6.14)

Уравнение (7.14) графически изображается прямой линией. Если по опытным данным построить график зависимости в двойных логарифмических координатах, то по нему можно определить искомые величины и (рис. 6.3).

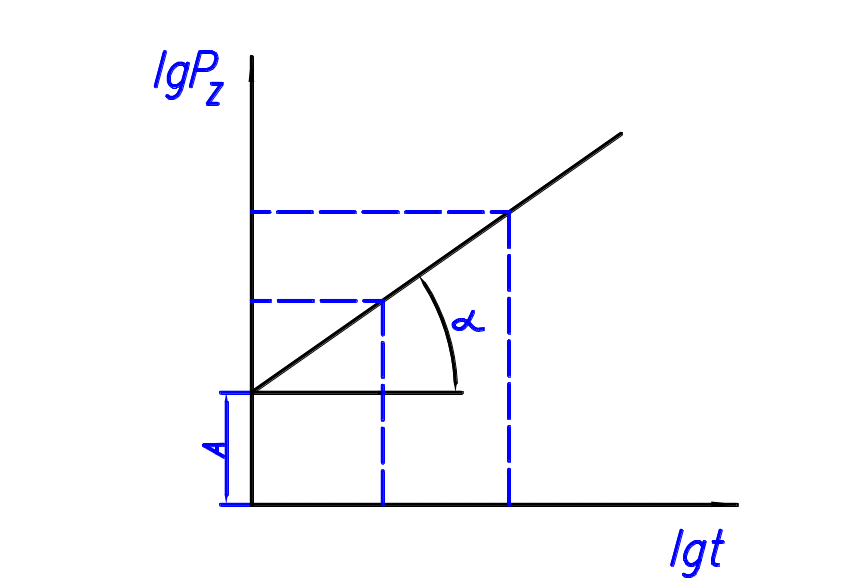
Рис. 6.3 График зависимости двойных логарифмов.

Величина соответствует отрезку оси ординат, отсекаемому прямой линией от начала координат, величина соответствует тангенсу угла наклона прямой к оси абсцисс: . Обрабатывая результаты опытов указанным методом, можно получить действительную зависимость . Аналогично получаются зависимости ; .

Зная значения составляющих сил резания для каждой комбинации значения параметров режима резания, рассчитать значения постоянной константы, подставив их в общее уравнение (6.15):

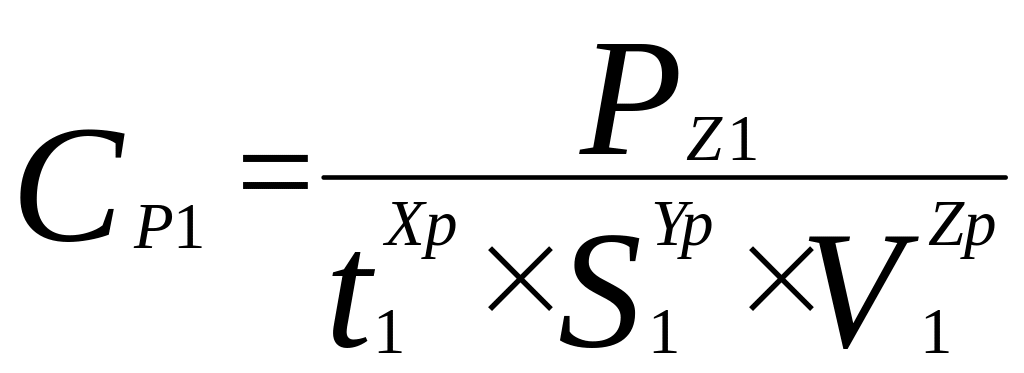(6.15)

По рассчитанным значениям констант рассчитать усредненное значение:

(6.16)

Для каждой комбинации параметров режима резания затем рассчитать с учетом значения составляющих силы резания.

. (6.17)

Рассчитать итоговую погрешность усредненной формулы.

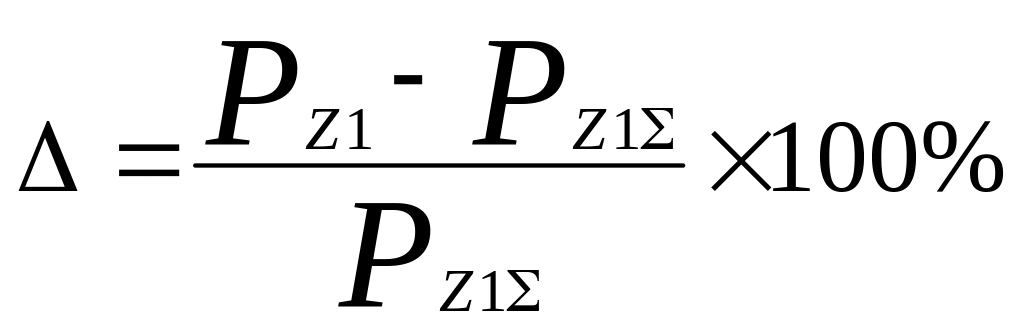. (6.18)

Приближение действительной к расчетной величине, рассчитанной по формуле считать удовлетворительной при .