27 Вопрос Фундаментальная система решения (фср) лосу. Теорема об общем решении лосу.
Тема об общем решении ЛОДУ n-ого порядка Ln[y]=0
…….
называются линейно независимыми на
отрезке( а,b),
если их линейная комбинация
+
тождественно
0 на отрезке ( a,b)
следовательно
В противном случае система называется линейно-зависимой.
называется
фундаментальной системой решения ЛОДУ
n-ого
порядка , если эти функции являются
решением ЛОДУ линейно-независимы на
отрезке (a,b).
Теорема об общем решении ЛОДУ.
Если
функция
обратная ФСР
ЛОДУ n-ого
порядка, то
=
(x)+
28 Вопрос. Решение лосу с постоянными коэффициентами методом Эйлера.
(1)
………………………………………
скалярная форма
записи.
Y’=AY (2)
Y=H* (3)
H=
Y’=
)’=H
( 4)
(3)(4)->(2): H =AH :
H
AH=
H
(A-
E=
Det(A-
)=0
(6)
=0
(7)
(7)-характеристическое уравнение.
Pn(
.Корни
могут быть, как действительные, так и
комплексные числа.
=
-
корень характеристического уравнения,
k=1
-соответствующий
собственный вектор ( опр из (5))
,
=
+
+…….+
Характеристическое уравнение для системы n-ого порядка всегда совпадает с характеристическим уравнением для ЛОДУ n-ого порядка.
p+iq-
корень характеристического уравнения
кратный k=1
=
p+iq
также -//-//-из (5)->H=V+Vi
V+Vi)
=ImY
линейно-независимые
на отрезке (a,b)
то общее решение однородной системы =
29 Вопрос.
Теорема об общем решении линейной неоднородной системы дифференциальных уравнений (ЛНСУ).
Общее решение линейной неоднородной системы дифференциальных уравнений является суммой общего решения соответствующего однородной системе и частного решения неоднородной системы.
=
+
=0
=F(x)
Для решения неоднородной системы можно использовать метод подбора частного решения и метод вариации произвольных постоянных.
30 Вопрос
Числовые ряды. Основные определения. Общие свойства рядов. Необходимые признаки сходимости рядов.
Рядом называется последовательность , объединенная знаком суммирования.
—
числовой
ряд
Сходимость числового ряда:
числовой ряд сходится, если сходится последовательность его частичных сумм;
числовой ряд расходится, если расходится последовательность его частичных сумм:
числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Если числовой ряд сходится, то предел S последовательности его частичных сумм носит название суммы ряда:
S=
Частичной суммой ряда называется сумма первых n членов ряда.
Сумма ряда определяется при помощи операции предельного перехода.
Суммой ряда называется предел частичной суммы при n->∞
называется
сходящимся, если существует конечный
предел его частичных сумм.
Ряд называется расходящимся, если предел его частичных сумм равен бесконечности или не существует.
Если ряд сходится, то придел его общего числа равен 0.
Общие свойства рядов.
и
сходятся, то
)
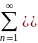и
также сходятся при этом
)=
±
2.Если
,
то
,
также сходится, и
=
А*
3.При добавлении в начало ряда, конечного числа членов или исключение конечного числа членов ряда .Новый ряд сходится или расходится одновременно с исходным.
̴ (ведут себя одинаково).
Необходимый признак сходимости ряда
Если ряд сходится, то предел его общего члена равен 0.
->
=
Следствие.
Достаточный признак расходимости ряда
Если члены ряда не стремятся к нулю, то ряд расходится.
Гармонический:
расходится , хотя
=0