3. Символьні та чисельні обчислення

Maple – це програмний пакет для автоматизації символьних, чисельних і графічних обчислень. Він може вирішувати як прості, так і досить складні завдання. Ну а якщо ви знаходилися в „кам’яному столітті” і вирішували ваші математичні і інженерні проблеми за допомогою мов програмування, то у вас з’явився реальний шанс потрапити відразу в століття XXI – в середу Maple, яка стала передвісником повернення математики і інженерної діяльності людини до епохи романтизму символьних обчислень минулих століть, коли геніальні відкриття здійснювали „на кінчику пера”. Широта функціональних можливостей Maple вражає – вона охоплює такі розділи, як лінійна алгебра, диференціальні обчислення, геометрія, статистика і багато іншого. По кожному розділу написана велика кількість процедур і функцій, якими можна скористатися, набравши ім’я однієї з них в командному рядку Maple.

Символьні обчислення. Maple видає відповідь в найточнішій формі — символьній, точнішій, ніж будь-який з чисельних методів. Проте, якщо ви хочете отримати відповідь у вигляді числа з плаваючою крапкою, то вона буде знайдена в кінці символьних обчислень. Таким чином, похибка методу – це лише похибка округлення! Розв’язання виходять компактними, можна сказати – витонченими.

Чисельні обчислення. Чисельні обчислення – альтернативний шлях знаходження розв’язку в тих випадках, коли символьний метод дуже довго працює над даним завданням або розв’язок в символьному вигляді взагалі не існує. Maple підтримує майже всі існуючі чисельні методи. Всі символьні константи можуть бути наближені з точністю до будь-якого знаку, оскільки середовище Maple має „ нескінченну точність ”[4].

Розділ 3 чисельний аналіз похибок обчислень значень похідних аналітичних функцій

1. Чисельне знаходження похідних аналітичних функцій

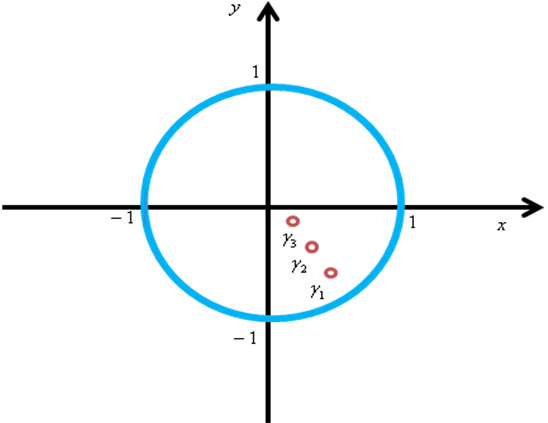
Розглянемо одиничний круг, в якому - послідовність точок, що збігаються до 0. Виберемо послідовність так, щоб і .

Позначимо через наближені значення похідних аналітичної функції в точці 0 одиничного круга. Цю послідовність будемо задавати поетапно, визначаючи на ому кроці зразу всі [7-9].

Нехай - значення функції в точці , а . Покладемо, що . Тоді елементи послідовності визначимо наступним чином:

… … … …

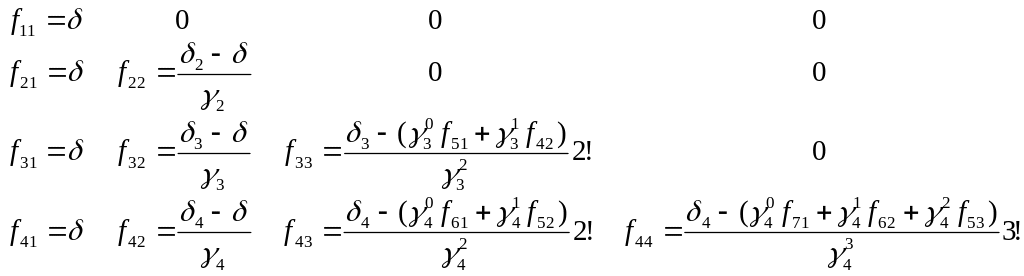В результаті отримаємо наступну формулу:

. (3.1)

Виразивши значення тільки через та , отримаємо наступні формули :

наближені значення першої похідної:

; (3.2)

наближені значення другої похідної:

; (3.3)

наближені значення третьої похідної:

, (3.4)

і так далі.

Знайдемо формулу для вираження наближених значень похідних аналітичних функцій (3.1) за допомогою послідовності коефіцієнтів, які задаються рекурентно. Введемо позначення :

… … … … …

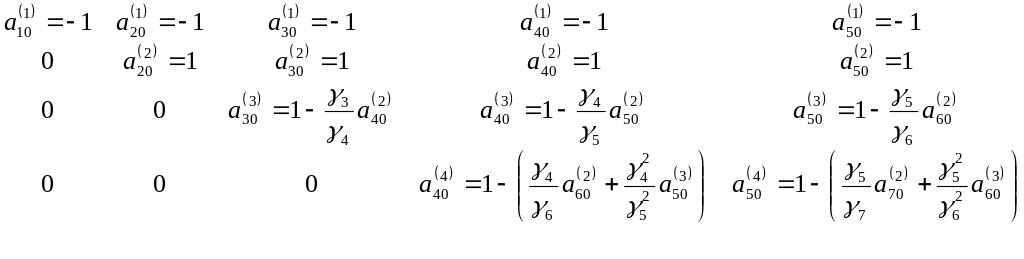Тоді отримаємо наступну формулу для знаходження коефіцієнтів:

. (3.5 )

Із формули (3.5) дістанемо формули для обчислення наближених значень похідних аналітичних функцій:

наближені значення першої похідної:

; (3.6)

наближені значення другої похідної:

; (3.7)

наближені значення третьої похідної:

; (3.8)

наближені значення четвертої похідної:

. (3.9)

Загальний вигляд формули для знаходження наближеного значення тої похідної аналітичної функції наступний:

, . (3.10)