2. Формули чисельного диференціювання для рівновіддалених вузлів

Якщо вузли інтерполяції розташовані через рівні проміжки, то зручніше використовувати відповідні інтерполяційні формули. Так, наприклад, взявши інтерполяційну формулу Ньютона для інтерполяції вперед

(1.6)

в результаті послідовного диференціювання отримаємо:

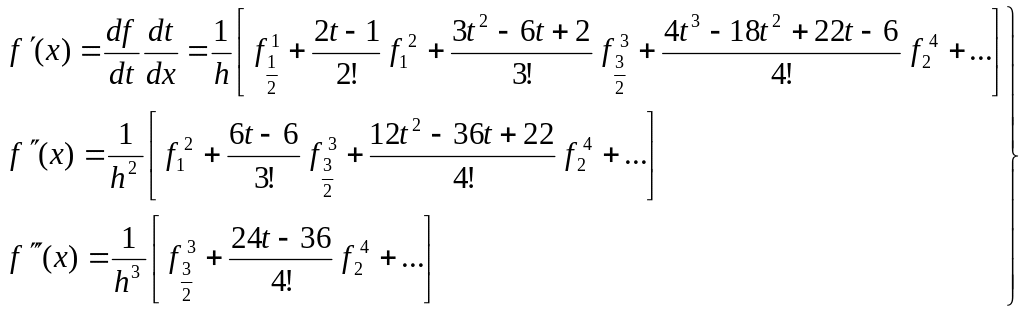
Зокрема, при х = х₀ будемо мати:

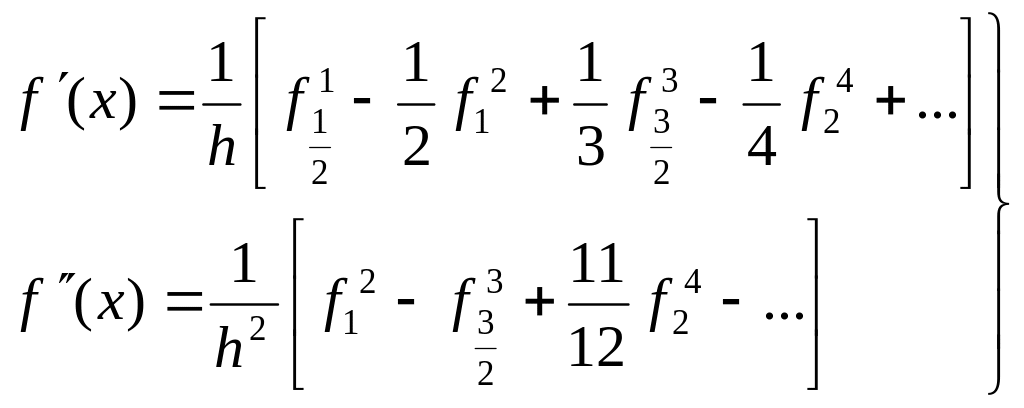(1.7)

Приклад 2. Знайти методом чисельного диференціювання похідні перших трьох порядків для многочлена в точці .

Складаємо таблицю різниць

x	f	f1	f2	f3
1 2 3 4 5	-6 -1 16 51 110	5 17 35 59	12 18 24	6 6

По отриманих формулах маємо:

,

,

.

Якщо використовувати інші формули інтерполювання, то можна отримати інші формули чисельного диференціювання. Візьмемо, наприклад, формулу Стірлінга

Послідовність похідних буде мати вигляд

При x=x₀

Якщо використати формулу Бесселя

,

то отримаємо:

і при x=x₀

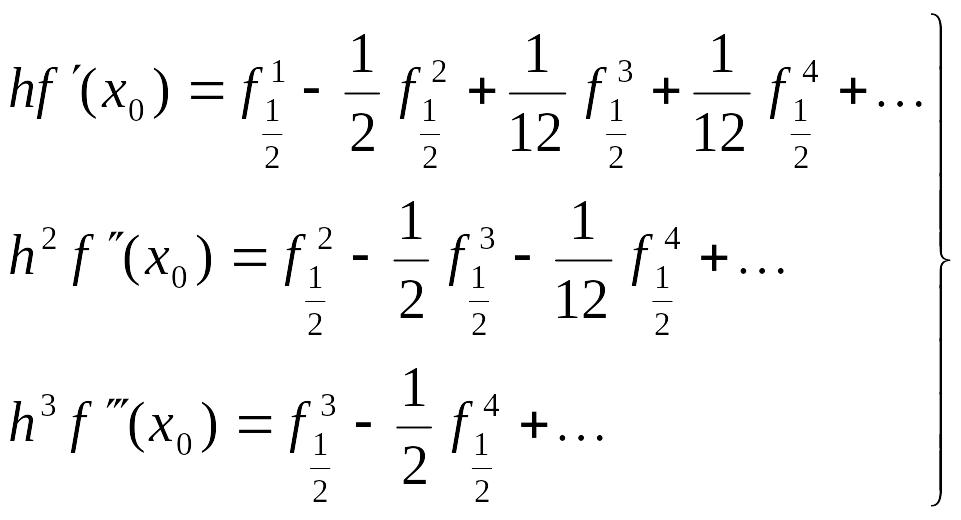
1.2.3. Без різницеві формули чисельного диференціювання

У деяких випадках вигідніше виражати формули чисельного диференціювання не через різниці, а безпосередньо через значення функції. Для отримання таких формул зручно скористатися варіантом формули Лагранжа для випадку рівних проміжків:

. (1.8)

Диференціюючи один раз, отримаємо:

.

При x = x_k будемо мати:

.

Для другої похідної будемо мати:

і при x = x_k:

.

Випишем готові вирази для похідних першого і другого порядку при різних п.

N=2 (три точки): ;

;

.

N=3 (чотири точки): ;

;

;

.

N=4 (п’ять точок): ;

; ;

;

.

Порівнюючи різні формули, ми бачимо, що найбільш простіші вираження отримуються при парних п у середніх точках. При цьому і коефіцієнти при похідних у залишкових членах будуть найменшими. Тому на практиці, по можливості, варто застосовувати ці формули.

Якщо навести відповідні вирази для других похідних, то і в цьому випадку найбільш вигідні формули отримуються для парних п і для середніх точок [15].

4. Метод невизначених коефіцієнтів

Можна отримати аналогічні формули і для довільного розташування вузлів. При цьому, щоб не обчислювати громіздкі вирази багаточлена Лагранжа, зручніше використовувати метод невизначених коефіцієнтів. Для цього записуємо шукану формулу у вигляді

(1.9)

і підбираємо коефіцієнти c_i з умови R(f)=0, коли . Отримаємо наступну систему для визначення коефіцієнтів c_i

,

,

...........................................

,

,

,

...........................................

.

1.3. Наближення похідної

Розглянемо числовий процес наближення похідної :

.

Метод виглядає просто – вибираємо послідовність так, що , і обраховуємо границю:

для .

Формула центральної різниці

Якщо функцію можна обчислити для значень, які лежать зліва і справа від , то найкраща двохточкова формула буде містити абсциси , які вибрані симетрично відносно .

Формула порядку .

Припустимо,що і що . Тоді

. (1.10)

Формула порядку .

Припустимо, що і що . Тоді

. (1.11)

Щоб отримати формули центрованих різниць для похідних вищих порядків можна використати ряд Тейлора. Найпоширеніші з вибраних порядків - і - наведені в таблиці 1.1 і 1.2. В таблицях використані позначення для .

Таблиця 1.1. Формула центрованої різниці порядку .

Таблиця 1.2. Формула центрованої різниці порядку .

Для ілюстрації отримаємо формулу для порядку з таблиці 1.1. Розпочнемо з розкладу Тейлора:

(1.12)

і

(1.13)

Сумуємо вирази (1.12) і (1.13), виключаємо члени,які містять непарні похідні :

. (1.14)

Виконуємо рівність (1.14) відносно і отримаємо

.(1.15)

Якщо розглядати ряд (1.15) до четвертої похідної, то існує таке значення с, яке лежить на інтервалі , що

. (1.16)

Це дає формулу для наближення :

. (1.17)

Диференціювання полінома Лагранжа.

Для обчислення значення функції в абсцисі, яка лежить з однієї сторони від точки , не можна використовувати формулу центрованої різниці. Формули для рівновіддалених абсцис, які лежать справа (або зліва) від точки , називають формулами для правих (або лівих) різниць. Ці формули можна отримати диференціюванням інтерполяційного многочлена Лагранжа [22]. Деякі загальні формули для правих і лівих різниць наведені в таблиці 1.3.

Таблиця 1.3. Формули для правих і лівих різниць порядку

	Права різниця
	Ліва різниця
	Права різниця
	Ліва різниця
	Права різниця
	Ліва різниця
	Права різниця
	Ліва різниця