Розділ 1 чисельне диференціювання

1.1. Задача чисельного диференціювання

До чисельного диференціювання доводиться звертатися в тому випадку, коли функція f(x), для якої потрібно знайти похідну, задана таблично або ж функціональна залежність х і f(х) має дуже складне аналітичне представлення. У першому випадку методи диференціального числення не застосовуються, а в другому випадку їхнє використання викликає значні труднощі.

У цих випадках замість функції f(х) розглядають інтерполяційну функцію, φ(х) і обраховують похідну від f(x), яка наближено рівна похідній від φ(х). При цьому похідна від f(х) буде знайдена з деякою похибкою.

Функцію f(x) можна записати в такому вигляді:

, (1.1)

де φ(х) — інтерполяційна функція, а R(x) — залишковий член інтерполяційної формули. Диференціюючи цю тотожність k разів (припускаючи, що f(х) і φ(х) мають похідні k-го порядку), одержимо:

. (1.2)

Оскільки за наближене значення f^(k)(x) приймається φ^(k)(x), то похибкою буде R^(k)(x). При заміні f(х) інтерполяційною функцією φ(х) припускають, що залишковий член невеликий, але з цього зовсім не випливає, що невелике R^(k)(x), тому що похідні від малої функції можуть бути досить великі. І насправді, практика показує, що при такому способі обчислення похідних f^(k)(x)) отримується порівняно велика похибка, особливо при обчисленні похідних вищих порядків.

Розглянемо формули диференціювання в загальному випадку, коли інтерполяційна функція φ(х) будується як лінійна комбінація базисних функцій φ₀(х), φ₁(х), ..., φ_n(х), які утворюють систему Чебишева на розглянутому відрізку [a,b].

Запишемо функцію f(х) у вигляді:

.

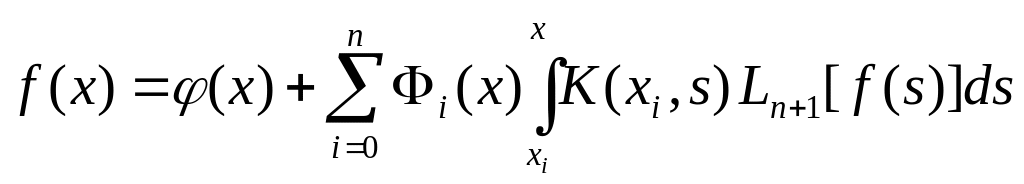Тут - інтерполяційний многочлен, — лінійна комбінація базисних функцій φ_k(х) (k = 0, 1, 2,..., п), які задовольняють умовам

де x_i – вузли інтерполювання,

,

.

Диференціюємо обидві частин рівності. Отримаємо:

.

Але

.

Таким чином,

.

При чисельному диференціюванні за наближене значення похідної беруть . Тоді другий член справа буде давати залишковий член.

Диференціюючи останню рівність ще раз, знайдемо:

І в цьому випадку

.

Тому

.

Знову перший член праворуч дає наближене значення похідної, а другий — залишковий член.

Ці міркування можна провести для похідних будь-якого порядку, меншого або рівного п.

З отриманих виразів залишкових членів видно, що формули чисельного диференціювання дають точне значення для похідних, якщо f(х) довільна лінійна комбінація базисних функцій φ₀(х), φ₁(х), ..., φ_n(х).[28]

1.2. Формули чисельного диференціювання

1.2.1. Формули чисельного диференціювання для не рівновіддалених вузлів

Будемо виходити з інтерполяційної формули Ньютона для нерівних проміжків:

. (1.3)

Для скорочення записів позначимо . Диференціюючи обидві частини рівності (1.3) один раз, будемо мати:

.

За наближене значення першої похідної при чисельному диференціюванні будемо приймати

.

Залишковий член буде мати вигляд:

,

Спростимо другий член справа. За означенням

.

Таким чином,

або, якщо використовувати зв'язок розділених різниць з похідними,

.

У вузлах інтерполяції x₀, x_{1, …,} х_п другий член праворуч перетворюється в нуль і вигляд залишкового члена буде більш простим. Диференціюючи ще раз, отримаємо:

.

За наближене значення другої похідної при чисельному диференціюванні будемо приймати

.

Залишковий член буде мати вигляд:

або

.

Якщо x приймає одне зі значень x₀, x_{1, …,} х_п , то останній член праворуч перетвориться в нуль і залишковий член спроститься. Аналогічні міркування можна провести і для будь-якого k ≤ п. В загальному випадку отримаємо:

.

Для спрощення залишкових членів нам знадобляться вираз

.

Покажемо, що

. (1.4)

Як це випливає з попереднього, при т= 1 і 2 ця формула справедлива. Припустимо, що вона справедлива при т = r, і доведемо її справедливість при т = r+1. За припущенням

і .

Скористаємось знову означенням похідної

Вираз в чисельнику останнього дробу можна записати у вигляді

.

Таким чином,

,

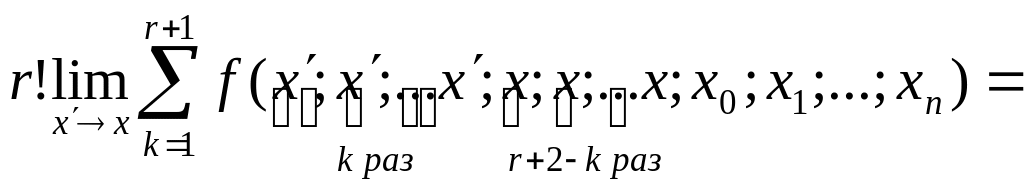
і формула (1.4) доведена. За цією формулою залишковий член при чисельному відшуканні похідної порядку k може бути представлений у вигляді

,

де - деякі точки, які знаходяться в інтервалі між найбільшим і найменшим з чисел x₀, x_{1, …,} х_п..

Якщо точка х знаходиться поза межами відрізка, що містить точки x₀, x_{1, …,} х_п , то залишковий член може бути записаний більш простим виразом. Для цього розглянемо многочлен .

Він співпадає з функцією f(х) у точках x₀, x_{1, …,} х_п . Підберемо сталу С так, щоб у точці х’, для якої знаходиться оцінка, мала місце рівність

. (1.5)

Це можливо, оскільки всі корені рівняння лежать у найменшому відрізку, що містить x₀, x_{1, …,} х_п. Розглянемо допоміжну функцію

.

Ця функція перетворюється в нуль у точках x₀, x_{1, …,} х_п. Відповідно, перша похідна її перетворюється на найменшому відрізку, що містить точки x₀, x_{1, …,} х_п, в нуль принаймні п разів. Проводячи ті ж міркування далі, одержимо, що похідна порядку k перетворюється на цьому відрізку в нуль принаймні п+1- k раз. Але опираючись на вибране с вона перетвориться в нуль і в точці х’, що лежить поза цим відрізком. Таким чином, вона перетвориться в нуль принаймні в п+2- k точках. Знову будемо послідовно застосовувати теорему Ролля. Зрештою, прийдемо до висновку, що похідна порядку п+1 перетвориться в нуль принаймні в одній точці . Але

Звідси

і .

Отримали більш просте представлення залишкового члена.

Розглянемо приклад на застосування формул чисельного диференціювання.

Приклад 1. По таблиці

x	10º	14º	16°	20°
sinx	0,173648	0,241922	0,275637	0,342020

використовуючи формули чисельного диференціювання, знайти соs 15° і sin 15°.

Складаємо таблицю розділених різниць:

xi	f(xi)	f(xi;xi+1)	f(xi;xi+1;xi+2)	f(xi;xi+1;xi+2;xi+3)
10° 14° 16° 20°	0,173648 0,241922 0,275637 0,342020	17068,50 16857,50 16595,75	-35,17 -43,62	-0,84

Звідси отримуємо, враховуючи, що в нашому випадку α₀ = 5, α ₂=1, α₃=-1:

.

Множник праворуч з’явився за рахунок того, що в нашому випадку х узяте в градусному вимірі. Точне значення із шістьма вірними знаками соs15°=0,965926. Використовуючи формулу для другої похідної, отримаємо:

.

Точне значення sin15° із шістьма знаками дорівнює 0,258819. Розбіжності вийшли досить значними. Це природно, тому що функції можуть бути і дуже близькими одна до одної, але мати похідні, які дуже відрізняються.

Проведемо оцінку точності. У першому випадку залишковий член буде мати такий вигляд:

.

При цьому

,

.

При х= 15° отримаємо: .

Таким чином, .

Ця величина значно менша фактично отриманої похибки. У даному випадку обчислена похибка значно перекриває похибку методу.

В другому випадку .

При цьому .

Таким чином, .

І в цьому випадку обчислена похибка дуже велика.