1. Марковский процесс: определение, свойства, представление.

Марковский процесс – для каждого момента времени вероятность любого состояния в будущем зависит только от ее состояния в настоящий момент времени и не зависит от того, каким образом система пришла в это состояние.

Характеристику процесса удобно представлять в виде графа состояний.

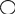- переходы

- состояния

S₁ – все работают

S₂ – 1 не работает, 2 работают

S₃ – 2 не работают, 1 работает

S₄ – 1,2 не работают

λ – интенсивность отказов

μ – интенсивность восстановления

Случайное событие – это событие, которое может появляться или не появляться в результате данного опыта.

Случайные события, следующие одно за другим в некоторой последовательности, образуют поток случайных событий.

Свойства:

1. Одинарный поток событий – поток, при котором вероятность попадания 2^х событий на один и тот же малый участок времени ∆t пренебрежимо мала.

2. Стационарный поток случайных событий – поток, однородный по времени, т.е. среднее число событий в единицу времени остается постоянным.

Поток без последействия – поток, для кот-го для 2^х непрерывающихся временных участков число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой участок.

2. Определение вероятностей состояний марковского процесса (вывод уравнений Колмогорова-Чепмена).

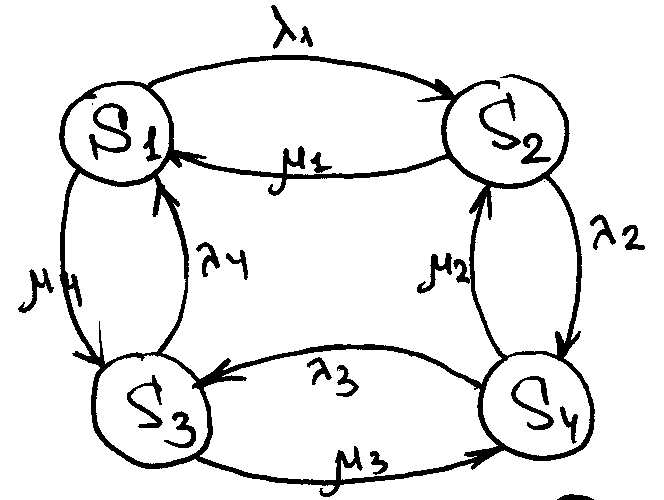
Вероятности того, что система будет находиться в i-том состоянии:

P₁(t+∆t)=p₁(t)p₁₁(∆t)+p₂(t)p₂₁(∆t)+p₃(t)p₃₁(∆t)

P₂(t+∆t)=p₂(t)p₂₂(∆t)+p₁(t)p₁₂(∆t)+p₄(t)p₄₂(∆t)

…

P_ij(∆t) – вероятность отказа

P_ji(∆t) – вероятность восстановления

P₁(t+∆t)=p₁(t)[1-(p₁₂(∆t)+p₁₃(∆t))]+…

при

1 – система работоспособна (единственное состояние)

2, 3, 4 – вероятность отказа системы

Р₁ – ВБР системы

В левой части производная по t для вероятности того, что мы определяем.

В правой части столько слагаемых, сколько входит и выходит стрелок («-» если стрелка выходит).

Если λ₁ = λ₂ = λ; μ₁ = μ₂ = μ

Если имеются 2 ремонтные бригады

S₁ – все работают

S₂ – 1 работает, 1 отказал

S₃ – все не работают

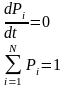
3. Правило получения уравнений Колмогорова-Чепмена непосредственно по виду графа состояний системы (на примере для системы, состоящей из двух элементов)

1. Для каждого из возможных состояний системы записываются уравнения, в левой части которого dPi/dt, а справа –только слагаемые, сколько стрелок графа соприкасается с данным состоянием.

2. Если стрелка направлена в данное состояние, то перед слагаемым ставиться +,если стрелка направлена из данного состояния- -.

3. Каждое из слагаемых будет равно произведению интенсивности перехода из данного состояния (либо в данное) на вероятности состояния, из которого выходит стрелка.

4-5. Решение уравнений Колмогорова-Чепмена для нестационарного и стационарного марковского процесса. Правило получения вероятностей состояний непосредственно по графу состояний. Вычисление стационарного коэффициента готовности и коэффициента простоя.

Для схемы, изображенной на рис.

а) число состояний – три. Состояние S_{0 ­}– два элемента, входящие в систему, работоспособны; состояние S₁ – один из элементов, входящих в систему , в неработоспособном состоянии; S₂ – оба элемента, входящие в систему, находятся в отказовом состоянии.

а ) б) 2 

 2

Получить систему дифференциальных уравнений можно непосредственно по виду графа переходов по следующему правилу.

1. Для каждого из возможных состояний системы записывается уравнение, в левой части которого - 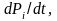а справа – столько слагаемых, сколько стрелок графа соприкасается с данным состоянием.

2. Если стрелка направлена в данное состояние, то перед слагаемым ставится плюс, если стрелка направлена из данного состояния – минус.

3. Каждое из слагаемых будет равно произведению интенсивности перехода из данного состояния (либо в данное состояние) на вероятности состояния, из которого выходит стрелка.

4. Вероятность нулевого состояния определяется выражением

5. Вероятность каждого из состояний определяется выражением:

.

Руководствуясь этим правилом, получим систему уравнения для нашего примера:

(7.2)

Решение уравнений можно получить, использовуя преобразование Лапласа. Основные соотношения преобразования приведены в табл.7.1.

Но с учетом того, что интенсивности переходов и постоянны и

равны соответственно: 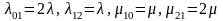, а рассматриваемый марковский процесс – процесс стационарный, решение системы уравнений можно существенно упростить, приняв производные равными нулю:

(7.3)

Четвертое уравнения системы (при трех неизвестных) становится необходимым потому, что первые три уравнения сводятся к двум. Решение этой системы будет иметь вид

, ,

.

Теперь нетрудно вычислить стационарные коэффициенты готовности и простоя системы. Коэффициент готовности представляет собой сумму вероятностей работоспособных состояний системы, в нашем примере

, .