Роль силы трения в быту

Роль силы трения в быту сводится к тому, что мы можем ходить и ездить, что предметы не выскальзывают у нас из рук, что полки и картины висят на стенах, а не падают, даже одежду мы носим благодаря трению, которое удерживает волокна в составе нитей, а нити в структуре тканей.

Но трение может играть и отрицательную роль. Именно из-за него нагреваются и изнашиваются движущиеся части различных механизмов. В таких случаях его стараются уменьшить. Существует несколько способов уменьшения трения.

Один из них – это введение смазки между трущимися поверхностями. Смазка уменьшает соприкосновение тел, и трутся не тела, а слои жидкости. А трение в жидкости намного меньше, чем сухое трение.

Еще примеры силы трения в быту:

• мы можем писать на бумаге

• вещи, стоящие на вашем столе, не улетают от малейшего сквозняка

• одежда, которая висит на вашем стуле или плечиках в шкафу

• вы можете водите компьютерной мышкой по коврику

• вы с трудом двигаете шкаф, т.к. есть сила трения

• но если случайно разлить подсолнечное масло на кухне, любой входящий будет скользить, т.к. уменьшится сила трения об пол, но аккуратнее, не упадите сами :)

• ковер сильно уменьшает силу трения

• смазывание петлей дверей

• музыкальные инструменты

Сила трения в технике

Еще одним способом уменьшить трение является применение шариковых и роликовых подшипников. Внутреннее кольцо подшипника одевается на вал какого-либо механизма, а наружное кольцо закрепляют в корпусе машины или станка. И когда вал начинает вращаться, то он не скользит, а катится на шариках или роликах между кольцами подшипника.

А мы знаем, что сила трения качения значительно меньше трения скольжения. Поэтому вращающиеся части изнашиваются гораздо медленнее. Применяют также воздушную подушку, уменьшение площади соприкасающихся тел, а также шлифовку.

Например, чтобы уменьшить силу трения между льдом и коньками, коньки точат, делая поверхность соприкосновения меньше, а лед шлифуют, делая его максимально гладким. Так же уменьшают трение при резке чего-либо в быту и на производстве, затачивая ножи как можно острее.

Роль силы трения в технике не всегда отрицательна, как могло показаться. Ведь, например, когда мы заменяем силу трения скольжения трением качения, чтобы уменьшить взаимодействие трущихся поверхностей, то следует помнить, что если бы трение отсутствовало совсем, то колеса или шарики в подшипниках просто-напросто прокручивались бы, не приводя тело в движение.

Еще примеры силы трения в технике:

• автомобиль может тормозить

• на севере люди передвигаются на санках и лыжах - так быстрее, т.к. меньше сила трения

• езда на велосипеде

• любые смазанные детали работают лучше

• в шарикоподшипниках возникает сила трения качения

• колеса с шипами или даже с цепями

• механизмы для передачи или преобразования движения с помощью трения, т.н. фрикционные механизмы

Роль силы трения в природе

Стоит упомянуть и о роли силы трения в природе. Пример – это шероховатые лапки насекомых для улучшения сцепления с поверхностью, или, наоборот, это гладкие тела рыб, покрытые слизью для уменьшения трения о воду.

В природе животные и растения давно научились приспосабливаться и использовать силу трения себе во благо. То же необходимо делать и человеку, дабы обеспечить себе комфортное существование на планете Земля.

Еще примеры силы трения в природе:

• мы можем ходить по земле

• белки прыгают по веткам деревьев

• ленивец висит на ветке

• птичка может присесть на ветку

• вода точит камень

• образование планет и комет

• идет дождь и вода стекает в низину, хотя камень лежит и не скатывается в низину (у воды сила трения меньше, чем у камня)

• огромные валуны лежат на краях скал и не падают вниз - их держит сила трения

8. Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.

Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия (другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).

Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется

пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.

Наиболее простые виды деформации тела в целом:

• растяжение-сжатие,

• сдвиг,

• изгиб,

• кручение.

В большинстве практических случаев наблюдаемая деформация представляет собой совмещение нескольких одновременных простых деформаций. В конечном счёте, однако, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.

Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки (то есть тело возвращается к первоначальным размерам и форме), и пластической, если после снятия нагрузки деформация не исчезает (или исчезает не полностью).

Все реальные твёрдые тела при деформации в большей или меньшей мере обладают пластическими свойствами. При некоторых условиях пластическими свойствами тел можно пренебречь, как это и делается в теории упругости. Твёрдое тело с достаточной точностью можно считать упругим, то есть не обнаруживающим заметных пластических деформаций, пока нагрузка не превысит некоторого предела (предел упругости).

Природа пластической деформации может быть различной в зависимости от температуры, продолжительности действия нагрузки или скорости деформации. При неизменной нагрузке, приложенной к телу, деформация изменяется со временем; это явление называется ползучестью. С возрастанием температуры скорость ползучести увеличивается. Частными случаями ползучести являются релаксация и упругое последействие. Одной из теорий, объясняющих механизм пластической деформации, является теория дислокаций в кристаллах.

Си́ла упру́гости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.

В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности.

Вектор силы противоположен направлению деформации тела (смещению его молекул). Если исчезает деформация тела, то исчезает и сила упругости.

В Международной системе единиц (СИ) сила упругости так же, как и все другие силы, измеряется в ньютонах (русское обозначение: Н; международное: N).

Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.

Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.

Q — механическое напряжение.

F — сила, возникшая в теле при деформации.

S — площадь.

Различают две составляющие вектора механического напряжения:

• Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается  ).

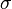• Касательное механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается  ).

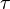Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.

В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёнымРобертом Гуком (Хуком) (англ. Robert Hooke)^[1]. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, направлена против смещения частиц тела при деформации и прямо пропорциональна удлинению.

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь   — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а   — коэффициент упругости(или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения   и длины  ) явно, записав коэффициент упругости как

Величина   называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука для относительных величин запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:

,

где   — жёсткость тела,   — величина деформации .

Жесткость тела зависит от формы и размеров, а также от материала, из которого оно изготовлено.

В словесной формулировке закон Гука звучит следующим образом:

Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации.