Виды равновесия

В механике различают три состояния  равновесия:  безразличного  равновесия,  устойчивого и неустойчивого равновесия.

Безразличное равновесие - при малом отклонении тело остается в равновесии. Пример - катящееся по горизонтальной поверхности колесо. Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия (рисунок).

Неустойчивое равновесие - при малом отклонение тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. Шар, находящийся в верхней точке сферического выступа, - пример неустойчивого равновесия .

Устойчивое равновесие - если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние. Шар, находящийся  на дне сферического углубления находится в состоянии устойчивого равновесия .

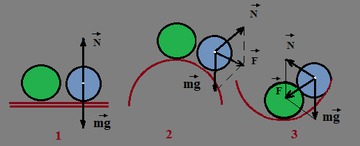
Рисунок  Различные виды равновесия шара на опоре. (1) - безразличное равновесие, (2) - неустойчивое равновесие, (3) - устойчивое равновесие

В неустойчивых системах при малом отклонениях тела от положения равновесия возникают силы, стремящиеся увеличить это отклонение.  Атом является неустойчивой системой, т.е при малейшем отклонении электрона вращающегося вокруг протона  (увеличение или уменьшение расстояния между протоном и электроном) центростремительные силы увеличивают это отклонение (подробнее см. Википедию).

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Общие сведения[править | править исходный текст]

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

где   — сила, действующая на частицу, а   — радиус-вектор частицы.

Предыстория[править | править исходный текст]

Строго говоря, вектор, обозначающий момент сил, введен искусственно^{[источник не указан 478 дней]}, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.

Работа, совершаемая при действии силы   на рычаг  , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок  , которому соответствует бесконечно малый угол  . Обозначим через   вектор, который направлен вдоль бесконечно малого отрезка   и равен ему по модулю. Угол между вектором силы   и вектором   равен  , а угол   между вектором   и вектором силы  .

Следовательно, бесконечно малая работа  , совершаемая силой   на бесконечно малом участке   равна скалярному произведению вектора   и вектора силы, то есть  .

Теперь попытаемся выразить модуль вектора   через радиус-вектор  , а проекцию вектора силы   на вектор  , через угол  .

Так как для бесконечно малого перемещения рычага  , можно считать, что траектория перемещения перпендикулярна рычагу  , используя соотношения для прямоугольного треугольника, можно записать следующее равенство:  , где в случае малого угла справедливо   и следовательно 

Для проекции вектора силы   на вектор  , видно, что угол  , а так как  , получаем, что  .

Теперь запишем бесконечно малую работу через новые равенства   или  .

Теперь видно, что произведение   есть не что иное как модуль векторного произведения векторов   и  , то есть  , которое и было принято обозначить за момент силы   или модуль вектора момента силы  .

Теперь полная работа записывается очень просто: 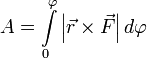  или 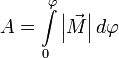 .