
- •4. Первый закон Ньютона
- •Современная формулировка[
- •Второй закон Ньютона
- •Третий закон Ньютона[
- •Центробежное ускорение
- •Гравитационное ускорение
- •Ускорение свободного падения на Земле
- •Измерение
- •Сила трения в природе
- •Роль силы трения в быту
- •Сила трения в технике
- •Роль силы трения в природе
- •9. Механическая работа и мощность
- •Кинетическая и потенциальная энергии
- •Закон сохранения механической энергии
- •История появления термина[править | править исходный текст]
- •Определение импульса в механике Ньютона[править | править исходный текст]
- •Обобщённый импульс в теоретической механике[править | править исходный текст]
- •Определение через волны де Бройля[править | править исходный текст]
- •Закон сохранения импульса в общей теории относительности[править | править исходный текст]
- •Абсолютно упругий удар
- •Момент силы и момент импульса относительно неподвижного начала
- •11. Условия равновесия тел
- •Виды равновесия
- •Общие сведения[править | править исходный текст]
- •Предыстория[править | править исходный текст]
- •Единицы[править | править исходный текст]
- •13. Агрегатные состояния вещества с точки зрения мкт
- •14. Идеальный газ
- •Скорость молекул газа
- •Основное уравнение мкт газа
- •Дополнительные расчетные формулы по теме
- •Шкала Кельвина
- •Шкала Цельсия
- •Шкала Фаренгейта
- •Шкала Реомюра
- •Графики изопроцессов
- •Сравнительная таблица графиков изопроцессов
- •Кипение жидкости
- •Зависимость температуры кипения от давления
- •19. Влажность воздуха
- •Точка росы
- •Измерение влажности
- •20. Свойства поверхности жидкостей. Поверхностное натяжение. Капиллярные явления.
- •21. Кристаллические и аморфные тела
- •Типы и виды кристаллов
- •Одномерные дефекты[править | править исходный текст]
- •Двумерные дефекты[править | править исходный текст]
- •Трёхмерные дефекты[править | править исходный текст]
- •Методы избавления от дефектов[править | править исходный текст]
- •Полезные дефекты[править | править исходный текст]
- •22. Внутренняя энергия тел и способы ее изменения.
- •Внутренняя энергия. Количество теплоты. Работа в термодинамике
- •Первый закон термодинамики
- •Частные случаи первого закона термодинамики для изопроцессов
- •Цикл Карно для тепловой машины
1.Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой.
В более общем значении движением называется изменение состояния физической системы с течением времени. Например, можно говорить о движении волны в среде.
Относительность движения
Два стрелка неподвижны относительно друг друга, но движутся, если рассматривать другие системы отсчёта.
Относительность — зависимость механического движения тела от системы отсчёта. Система отсчета представляет собой совокупностьсистемы координат для определения положения тела в пространстве и часов для определения времени. Не указав систему отсчёта, не имеет смысла говорить о движении.
s -
перемещение; вектор, соединяющий
начальную и конечную точки
движения.
Проекция вектора
перемещения на данную ось: sx =
x - x0.
Путь
(l)
- длина траектории.
|
v - скорость равноверного движения; мгновенная скорость; конечная скорость в равноускоренном движении |
м/с |
v0 - начальная скорость в равноускоренном движении |
м/с |
|
s - перемещение тела |
м |
|
t - время движения |
с |
|
a - ускорение |
м/с2 |
|
vср - средняя скорость |
м/с |
|
F - сила |
Н |
|
А - работа силы |
Дж |
|
l - путь тела |
м |
|
|
|
Ско́рость (часто
обозначается ![]() ,
от англ. velocity или фр. vitesse) — векторная физическая величина,
характеризующая быстроту перемещения и
направление движения материальной
точки относительно
выбранной системы
отсчёта;
по определению, равна производной радиус-вектора точки
по времени[1].
Этим же словом называют и скалярную величину
— либо модуль вектора
скорости, либо алгебраическую
скорость точки,
т. е. проекцию этого вектора на
касательную к траектории точки[2].
,
от англ. velocity или фр. vitesse) — векторная физическая величина,
характеризующая быстроту перемещения и
направление движения материальной
точки относительно
выбранной системы
отсчёта;
по определению, равна производной радиус-вектора точки
по времени[1].
Этим же словом называют и скалярную величину
— либо модуль вектора
скорости, либо алгебраическую
скорость точки,
т. е. проекцию этого вектора на
касательную к траектории точки[2].
Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят обугловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.
Обобщениями понятия скорости является четырёхмерная скорость, или скорость в релятивистской механике, и обобщённая скорость, или скорость в обобщённых координатах.
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
![]()
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей[1].
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.
Пусть
МТ в некоторый момент времени находилась
в точке А, а через промежуток
времени ![]() оказалась
в точке В (см. рис.). Тогда её перемещение
относительно системы К (абсолютное
перемещение) будет равно
оказалась
в точке В (см. рис.). Тогда её перемещение
относительно системы К (абсолютное
перемещение) будет равно ![]() .
Точка А подвижной системы K' за время
переместилась вместе с K' и оказалась в
точке С, совершив перемещение относительно
системы К (переносное перемещение),
изображённое на рисунке вектором
.
Точка А подвижной системы K' за время
переместилась вместе с K' и оказалась в
точке С, совершив перемещение относительно
системы К (переносное перемещение),
изображённое на рисунке вектором ![]() .
С точки зрения наблюдателя, связанного
с системой K', точка С является той точкой,
в которой МТ находилась первоначально,
поэтому вектор
представляет
собой перемещение МТ относительно
подвижной системы K', то есть относительное
перемещение. Из сказанного и векторной
диаграммы на рисунке следует
.
С точки зрения наблюдателя, связанного
с системой K', точка С является той точкой,
в которой МТ находилась первоначально,
поэтому вектор
представляет
собой перемещение МТ относительно
подвижной системы K', то есть относительное
перемещение. Из сказанного и векторной
диаграммы на рисунке следует
![]()
Деля данное равенство на промежуток времени , а затем устремляя его к нулю, в пределе получаем
![]()
где ![]() —
абсолютная,
—
абсолютная, ![]() —
переносная, а
—
переносная, а ![]() —
относительная скорость движения МТ.
—
относительная скорость движения МТ.
Полученное равенство является математическим выражением теоремы о сложении скоростей, которая формулируется так:
2. Прямолинейное равноускоренное движение – самый простой вид неравномерного движения, при котором тело движется вдоль прямой линии, а его скорость за любые равные промежутки времени меняется одинаково.
Равноускоренное движение – это движение с постоянным ускорением.
Ускорение тела при его равноускоренном движении – это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло:
→ → → v – v0 a = ——— t
Вычислить ускорение тела, движущегося прямолинейно и равноускоренно, можно с помощью уравнения, в которое входят проекции векторов ускорения и скорости:
vx – v0x ax = ——— t
Единица ускорения в СИ: 1 м/с2.
Применяются и другие единицы ускорения – например: 1см/с2.
Скорость прямолинейного равноускоренного движения.
vx = v0x + axt
где v0x – проекция начальной скорости, ax – проекция ускорения, t – время.
→ Если в начальный момент тело покоилось, то v0 = 0. Для этого случая формула принимает следующий вид:
vx = axt
3.
Равноме́рное движе́ние — механическое
движение,
при котором тело за любые равные отрезки
времени проходит одинаковое расстояние.
Равномерное движениематериальной
точки —
это движение, при котором
величина скорости точки
остаётся неизменной. Расстояние,
пройденное точкой за время ![]() ,
задаётся в этом случае формулой
,
задаётся в этом случае формулой ![]() .
.
Равномерное прямолинейное движение
Равномерное Прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковыеперемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.
![]() .
.
Если
направить координатную ось вдоль прямой,
по которой движется точка, то зависимость
координаты ![]() точки
от времени является линейной:
точки
от времени является линейной:
![]() ,
,
где ![]() —
начальная координата точки,
—
начальная координата точки, ![]() —
проекция вектора скорости на координатную
ось.
—
проекция вектора скорости на координатную
ось.
По определению инерциальной системы отсчёта, точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если векторная сумма всех сил, приложенных к точке, равна нулю.
Равномерное движение по окружности[
При
равномерном движении точки по окружности
её траекторией является дуга. Точка
движется с постоянной угловой
скоростью ![]() ,
а зависимость угла поворота точки от
времени является линейной:
,
а зависимость угла поворота точки от
времени является линейной:
![]() ,
,
где ![]() —
начальное значение угла поворота.
—
начальное значение угла поворота.
Эта
же формула определяет угол поворота абсолютно
твёрдого тела при
его равномерном вращении вокруг
неподвижной оси, то есть при вращении
с постоянной угловой скоростью ![]() .
.
Важной характеристикой данного типа движения является линейная скорость материальной точки
Нужно помнить, что равномерное движение по окружности — движение равноускоренное. Хотя модуль линейной скорости и не меняется, но меняется направление вектора линейной скорости (из-за нормального ускорения).
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
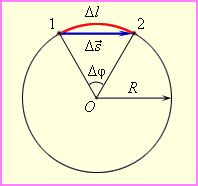
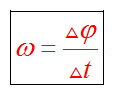

Период и частота
Период вращения T - это время, за которое тело совершает один оборот.
Частота вращение - это количество оборотов за одну секунду.
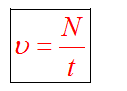

Частота и период взаимосвязаны соотношением
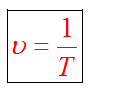
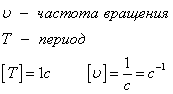
Связь с угловой скоростью
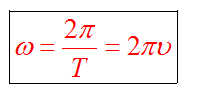

Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено - это есть период T. Путь, который преодолевает точка - это есть длина окружности.
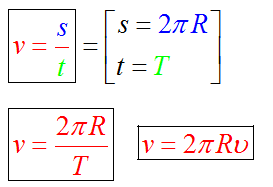

Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
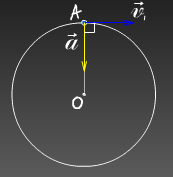
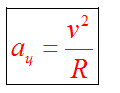
Используя предыдущие формулы, можно вывести следующие соотношения
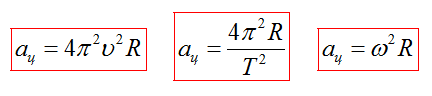
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
4. Первый закон Ньютона
Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как Закон инерции. Инерция — это свойство тела сохранять свою скорость движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность — это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела.
Современная формулировка[
В современной физике первый закон Ньютона принято формулировать в следующем виде[3]:
-
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся[1][2]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике[3]: «Инерциальной называется система отсчёта, по отношению к которой пространствоявляется однородным и изотропным, а время — однородным». Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта[4].
Термин «инерциальная система» (нем. Inertialsystem) был предложен в 1885 году Людвигом Ланге[en] и означал систему координат, в которой справедливы законы Ньютона. По замыслу Ланге, этот термин должен были заменить концепцию абсолютного пространства, подвергнутую в этот период уничтожающей критике. С появлением теории относительности понятие было обобщено до «инерциальной системы отсчёта».
Всякая система отсчёта, движущаяся относительно ИСО равномерно, прямолинейно и без вращения, также является ИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантны относительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядят одинаково, и записи этих законов имеют одинаковую форму в разных ИСО.
Предположение о существовании хотя бы одной ИСО в изотропном пространстве приводит к выводу о существовании бесконечного множества таких систем, движущихся друг относительно друга равномерно, прямолинейно и поступательно со всевозможными скоростями. Если ИСО существуют, то пространство будет однородным и изотропным, а время — однородным; согласно теореме Нётер, однородность пространства относительно сдвигов даст закон сохранения импульса, изотропность приведёт к сохранениюмомента импульса, а однородность времени — к сохранению энергии движущегося тела.
Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.
В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «c»(скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца.
Принцип относительности в классической механике
Впервые этот принцип был установлен Галилеем, но окончательную формулировку получил лишь в механике Ньютона. Для его понимания нам потребуется ввести понятиесистемы отсчета, или координат. Как известно, положение движущегося тела в каждый момент времени определяется по отношению к некоторому другому телу, которое называется системой отсчета. С этим телом связана соответствующая система координат, например, привычная нам декартова система. На плоскости движение тела или материальной точки определяется двумя координатами: абсциссой х, показывающей расстояние точки от начала координат по горизонтальной оси, и ординатой у, измеряющей расстояние точки от начала координат по вертикальной оси. В пространстве к этим координатам добавляется третья координата z.
Среди систем отсчета особо выделяют инерциальные системы, которые находятся друг относительно друга либо в покое, либо в равномерном и прямолинейном движении. Особая роль инерциальных систем заключается в том, что для них выполняется принцип относительности.
Принцип относительности означает, что во всех инерциальных системах все механические процессы происходят одинаковым образом. |
В таких системах законы движения тел выражаются той же самой математической формой, или, как принято говорить в науке, они являются ковариантными. Действительно, два разных наблюдателя, находящихся в инерциальных системах, не заметят в них никаких изменений.
5. Ма́сса (от греч. μάζα — «кусок теста») — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес.
В современной физике понятие «количество вещества» имеет другой смысл, а масса тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). Масса проявляется в природе несколькими способами.
Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная кмассивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений[1][2].
Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы)[3].
Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

 -
Путь l может
не совпадать по величине с
перемещением s.
Формулы
перемещения:
П
-
Путь l может
не совпадать по величине с
перемещением s.
Формулы
перемещения:
П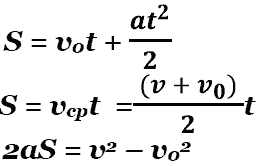 еремещение
при равноУскоренном движении.
Другие
формулы, где встречается
перемещение:
еремещение
при равноУскоренном движении.
Другие
формулы, где встречается
перемещение:
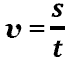 Скорость
при равноМерном движении.
Скорость
при равноМерном движении.