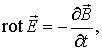25. Циркуляция и ротор электрического поля. Вихревое электрическое поле.

Теорема о циркуляции магнитного поля — Уравнение, представляющее собой содержание теоремы в этом обобщенном виде, входит в число уравнений Максвелла .Теорема гласит^[1]: Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

М атематическая формулировка

Здесь   — вектор магнитной индукции,   — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме^[4]:

Р отор— векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:

где i, j и k — единичные орты для осей x, y и z соответственно.

Э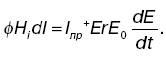 лектрическое поле, возникающее при изменении магнитного поля, имеет совсем другую структуру, чем электростатическое. Оно не связано непосредственно с электрическими зарядами, и его линии напряженности не могут на них начинаться и кончаться. Они вообще нигде не начинаются и не кончаются, а представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Это так называемое вихревое электрическое поле.

1. Всякое перемещенное электрическое поле порождает вихревое магнитное поле. Переменное электрическое поле было названо Максвеллом, так как оно, подобно обычному току, вызывает магнитное поле. Вихревое магнитное поле порождается как токами проводимости Iпр (движущимися электрическими зарядами), так и токами смещения (перемещенным электрическим полем Е).

Первое уравнение Максвелла

2 . Всякое перемещенное магнитное поле порождает вихревое электрическое (основной закон электромагнитной индукции).

Второе уравнение Максвелла:

26. Ток смещения.Если переменное магнитное поле создает поле электрическое, то разумно предположить существование и обратного процесса: изменяющееся электрическое поле порождает поле магнитное. -в диэлектриках

27. Электромагнитное поле

        особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами. Э. п. в вакууме характеризуется вектором напряжённости электрического поля Е и магнитной индукцией В, которые определяют силы, действующие со стороны поля на неподвижные и движущиеся заряженные частицы.

Диф. Форма:

     

     

     

Интеграл форма:

,

     

     

28.Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором он находился в первоначальный момент, выбранный произвольно).

Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярнаявеличина, размерность которой совпадает с размерностью определяемой физической величины.

Частота колебаний

        число полных колебаний в единицу времени. Для гармонических колебаний Ч. к. f = 1/T, где Т — период колебаний. Единица Ч. к. — одно колебание в секунду, или Герц. Часто пользуются величиной ω = 2πf, которая называется циклической или круговой частотой.

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:

Фа́за колеба́ний — физическая величина, используемая по преимуществу для описания гармонических или близких к гармоническим^[1][2]колебаний, меняющаяся со временем (чаще всего равномерно растущая со временем), при заданной амплитуде (для затухающих колебаний - при заданной начальной амплитуде и коэффициенте затухания) определяющая состояние колебательной системы в (любой) данный момент времени.^[3] Равно применяется для описания волн, главным образом - монохроматических или близких к монохроматичности.

Ма́ятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.

математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомойнерастяжимой нити или на невесомом стержне в поле тяжести.

 Физический маятник — твёрдое тело, совершающее колебания в поле каких-либосил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.

 Пружинный маятник — это груз, подвешенный на пружине и способный колебаться вдоль вертикальной оси.

Формула Томсона:

29.Собственными называются колебания системы – осциллятора - под действием лишь внутренних сил без внешних воздействий.

2-й закон Ньютона ma = F.

Учитывая, что ускорение есть вторая производная от смещения по времени , а сила, действующая на тело, есть сила упругости, определяемая для малых смещений тела от положения равновесия по закону Гука, как  , получим

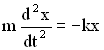или .

Перенесем все члены уравнения в левую часть и приведем дифференциальное уравнение к виду:

Величина  , обозначим ее  , получим

Решением дифференциального уравнения такого вида являются уравнения: или

 

30 .Затухающие гармонические колебания- колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.

Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как   (1) где s – колеблющаяся величина, которая описывает тот или иной физический процесс, δ = const — коэффициент затухания, ω₀ - циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.  Решение уравнения (1) запишем в виде :  (2) где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем   (3)  Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положителньного коэффициента:   (4)  (если (ω₀² - σ²)>0, то такое обозначение мы вправе сделать). Тогда получим выражение   , у которого решение будет функция   . 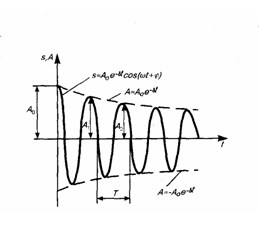Значит, решение уравнения (1) в случае малых затуханий (ω₀² >> σ² )   (5) где   (6) — амплитуда затухающих колебаний, а А₀ — начальная амплитуда. Выражение (5) представлено графики рис. 1 сплошной линией, а (6) — штриховыми линиями. Промежуток времени τ = 1/σ, в течение которого амплитуда затухающих колебаний становится мешьше в е раз, называется временем релаксации. 

период затухающих колебаний :  

Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, которые отличаются на период, то отношение   называется декрементом затухания, а его логарифм   (7) — логарифмическим декрементом затухания; N_e — число колебаний, которые совершаются за время уменьшения амплитуды в е раз. Логарифмический декремент затухания является постоянной величиной для данной колебательной системы. ДЕКРЕМЕНТ ЗАТУХАНИЯ (логарифмический декремент затухания) - количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону.

31.Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы F(t), периодически изменяющейся во времени ( так называемой вынуждающей силы).

Второй закон Ньютона для вынужденного колебания запишется в виде:  . Если ввести обозначения:   и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже полученоздесь и оно имеет вид:

,

где   — произвольные постоянные, которые определяются из начальных условий.

Найдём частное решение. Для этого подставим в уравнение решение вида:   и получим значение для константы:

Тогда окончательное решение запишется в виде:

Частота установившихся вынужденных колебаний совпадает с частотой ω вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости:

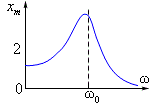
Резона́нс— явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

32.Процесс распространения колебании в сплошной среде называется волновым процессом ( или волной). Уравнение плоской одномерной волны

 Составим уравнение, которое позволит находить смещение всякой точки волны в любой момент времени. Пусть в точке В рис.8.2 находится источник колебаний. Волны со скоростью v распространяются от источника колебаний вдоль прямой.

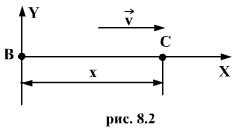
Уравнение колебаний точки В задано в виде: >

Все точки вправо от В, например точка С, повторяют колебания точки В с некоторым запозданием. Напишем уравнение колебаний точки С. Если точка В колеблется в течении времени t, то колебания дойдут до точки С по истечении времени  , поэтому время колебаний точки С будет меньше t и составит (t-t’) . Тогда уравнение колебаний точки С запишется:

Расстояние от точки В до точки С, равное х, волна проходит со скоростью  , откуда  . С учетом t’ уравнение волны будет иметь вид:

 (8.2)

,где λ - длина волны

Обозначим  эта величина называется волновым числом. Тогда получим следующее уравнение

 (8.3) которое называется уравнением плоской одномерной волны и определяет смещение любой точки среды, находящейся на расстоянии х от излучателя в данный момент. Величина

называется фазой волны.

ФРОНТ ВОЛНЫ, контур в пределах электромагнитного поля или материальной среды, все точки которого имеют одинаковые фазы колебаний. Фронт волны, как правило, перпендикулярен направлению распространения волны; он может быть плоским, сферическим или иметь более сложную форму. Каждая точка фронта является источником вторичных волн, которые через короткое время образуют фронт волны на новом месте.

33.Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.

Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

Свойства:

Частота - количество оборотов биона в единицу времени.

Скорость света - скорость передачи вращений от одного биона к другому.

Фаза - расположение одного из полюсов биона относительно линии распространения электромагнитной волны.

Дифракция электромагнитных волн - огибание волной края препятствия, наблюдаемое при малых по сравнению с длиной волны размерах препятствий.

Интерференция - явление взаимодействия в пространстве нескольких (двух или более) когерентных волн, при котором имеется усиление или ослабление результирующей волны в зависимости от того, в какой фазе волна оказывается в данной точке пространства.

Плоская электромагнитная волна - электромагнитная волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной направлению ее распространения, соответствуют одинаковые напряженности электрических или магнитных полей.

Электромагнитные волны классифицируются по длине волны или связанной с ней частотой волны.Спектр электромагнитного излучения в порядке увеличения частоты составляют:

1) Низкочастотные волны;2) Радиоволны;3) Инфракрасное излучение;4) Световое излучение;

5) Рентгеновское излучение;6) Гамма излучение.

Низкочастотные волны представляют собой электромагнитные волны, частота колебаний которых не превышает 100 КГц).Радиоволны представляют собой электромагнитные волны, длины которых превосходят 1 мм.Рентгеновское излучение составляют электромагнитные волны с длиной от50 нм до 10-3нм.Оптический спектр занимает диапазон длин электромагнитных волн в интервале от 210-6м= 2мкм до 10-8м=10нм

34.Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

КОГЕРЕНТНОСТЬ– согласованное протекание в пространстве и во времени нескольких колебательных или волновых процессов, при котором разность их фаз остается постоянной .Это означает, что волны (звук, свет, волны на поверхности воды и пр.) распространяются синхронно, отставая одна от другой на вполне определенную величину.

Условия максимумов и минимумов .Если оптическая разность хода равна целому числу длин волн в вакууме то , и колебания, возбуждаемые в точке М обеими волнами, будут

происходить в одинаковой фазе. Следовательно, является условием интерференционного максимума.Если оптическая разность хода ,то , и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следоательно, является условием интерференционного минимума.

35.Первые представления о природе света возникли у древних греков и египтян. По мере изобретения и совершенствования различных оптических приборов (параболического зеркала, микроскопа, зрительной трубы) эти представления развивались и трансформировались. В конце XVII века возникли две теории света: корпускулярная (И. Ньютон) и волновая.

Законы геометрической оптики

Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:

n = n2 / n1.

Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:

Принцип Гюйгенса.    Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени .

Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.

Из теории Гюйгенса вытекает закон отражения света: луч падающий, луч отраженный и нормаль к отражающей поверхности в точке падения лежат в одной плоскости, причем угол падения равен углу отражения..угол отражения равен углу падения: =;

36. Интерференция света — перераспределение интенсивности света в результате наложения(суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Призма Френеля. Линза Френе́ля — сложная составная линза. Состоит не из цельного шлифованного куска стекла со сферической или иными поверхностями (как обычные линзы), а из отдельных примыкающих друг к другу концентрических колец небольшой толщины, которые в сечении имеют форму призм специального профиля. Число полос N=4abφ²/ λ₀(a+b).

Зеркала Френеля — оптическое устройство, для наблюдения явления интерференции когерентных световых пучков. Устройство состоит из двух плоских зеркал I и II, образующих двугранный угол, отличающийся от 180° всего на несколько угловых мин. При освещении зеркал от источника S отражённые от зеркал пучки лучей можно рассматривать как исходящие из когерентных источников S1 и S2, являющихся мнимыми изображениями S. В пространстве, где пучки перекрываются, возникает интерференция. Если источник S линеен (щель) и параллелен ребру Ф. з., то при освещении монохроматическим светом интерференционная картина в виде параллельных щели равностоящих тёмных и светлых полос наблюдается на экране М, который может быть установлен в любом месте в области перекрытия пучков. По расстоянию между полосами можно определить длину волны света. Опыты, проведённые с Ф. з., явились одним из решающих доказательств волновой природы света. Число наблюдаемых интерференционных волн N найдем, разделив эту длину на ширину полосы ∆x. В результате получим: N=4φ²br / λ₀ (r+b).

Кольца Ньютона.Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами

Тонкие пленки.

 Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга^[1]. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной  , отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при  , где   — длина волны. Если   нм, то толщина плёнки равняется 550:4=137,5 нм.

Условие max и min.

Произведение геометрической длины s пути световой волны в данной среде на показатель nпреломления этой среды называется оптической длиной пути L, a  = L₂ – L₁ - разность оптических длин проходимых волнами путей - называется оптической разностью хода. Если оптическая разность хода равна целому числу длин волн в вакууме

                                    (172.2)

то  = ±2m, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, (172.2) является условием интерференционного  максимума.

Если оптическая разность хода

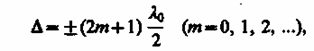                      (172.3)

то  = ±(2m + 1), и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следовательно, (172.3) является условием интерференционного минимума.