15. Закон Джоуля-Ленца в интегральной и дифференциальной формах.

Закон Джоуля - Ленца. Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, прямопропорционально произведению квадрата силы тока на этом участке и сопротивлению участка:

В математической форме этот закон имеет вид:

(дифференциальная форма)

(интегральная форма)

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t₁ доt₂.

16. Электрический ток в вакууме, газах. Понятие о плазме.

Электрический ток в вакууме.

Вакуум - это такая степень разрежения газа, при которой соударений молекул практически нет; - электрический ток невозможен, т.к. возможное количество ионизированных молекул не может обеспечить электропроводность; - создать эл.ток в вакууме можно, если использовать источник заряженных частиц; - действие источника заряженных частиц может быть основано на явлении термоэлектронной эмиссии.

Термоэлектронная эмиссия - это испускание электронов твердыми или жидкими телами при их нагревании до температур, соответствующих видимому свечению раскаленного металла. Электрический ток в вакууме возможен в электронных лампах. Электронная лампа - это устройство, в котором применяется явление термоэлектронной эмиссии. 

Электрический ток в газах.

В обычных условиях газ - это диэлектрик, т.е. состоит из нейтральных атомов и молекул и не содержит свободных носителей эл.тока

Газ-проводник - это ионизированный газ. Ионизированный газ обладает электронно-ионной проводимостью

Плазма.

Плазма- это четвертое агрегатное состояние вещества с высокой степенью ионизации за счет столкновения молекул на большой скорости при высокой температуре; встречается в природе: ионосфера - слабо ионизированная плазма, Солнце - полностью ионизированная плазма; искусственная плазма - в газоразрядных лампах.

Плазма бывает:

Низкотемпературная - при температурах меньше 100 000К; высокотемпературная - при температурах больше 100 000К.

17. Магнитное поле (мп) в вакууме. Взаимодействие токов. Вектор магнитной индукции. Принцип суперпозиции мп. Закон Био-Савара-Лапласа.

Магнитное поле – это особый вид материи,который возникает в окружении движущихся зарядов и проявляется в силовом воздействии на движущиеся заряды,помещенные в него.

Электрическое взаимодействие токов зависит от наличия зарядов и от их величины.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции  В.Модуль вектора магнитной индукции определяется отношением максимальной силы,действйющей со стороны магнитного поля на отрезок проводника с током,к произведению силы тока на длину этого отрезка:

18.Сила  , действующая на заряженную частицу, движущуюся в магнитном поле:

Зако́н Ампе́ра  — закон взаимодействия электрических токов. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила  , с которой магнитное поле действует на элемент объёма  проводника с током плотности  , находящегося в магнитном поле с индукцией  :

.

19. На рамку с током I, помещенную во внешнее однородное магнитное поле с индукцией   действует момент сил   Момент сил выражается соотношением: 

M = I S B sin α = pmB sin α ,

г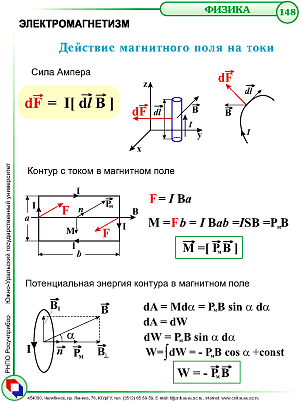 де S – площадь рамки, α – угол между нормалью   к плоскости рамки и вектором   Векторная величина   где   – единичный вектор нормали, называется магнитным моментом рамки. Направление вектора   связано с направлением тока в рамке правилом правого винта.

Полный момент силы, действующий на контур с током в магнитном поле, численно равен:  .

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.

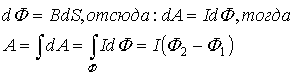
20. Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

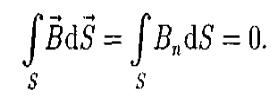
Циркуляцией вектора В по заданному замкнутому контуру называется интеграл:

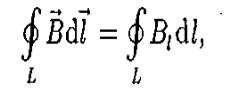где df — вектор элементарной длины контура, направленной вдоль обхода контура; Bl= В cos a — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода); а — угол между век-

торами В и df.

21. явление электромагнитной индукции. Онозаключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Правило Ленца. правило Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

, где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока.

ЭДС.Электродвижущая сила— скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

Закон Фарадея-Ленца утверждает,что.ЭДС индукции равна скорости изменения магнитного потока, взятой с обратным знаком.Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

• г 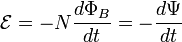де— число витков,

• — электродвижущая сила,

• — магнитный поток через один виток,

• — потокосцепление катушки.

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру.

При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током).

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока

Коэффициент пропорциональности L называется коэффициентом самоиндукции или индуктивностью контура (катушки).

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.

В формуле , Ф-магнитный поток, I — ток в контуре, L— индуктивность.

22.ток при размыкании и замыкании цепи с индуктивностью.энергия магнитного поля.

р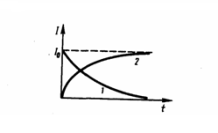 ассмотрим процесс выключения .В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома

Разделив в выражении переменные, получим Интегрируя это уравнение по I (от I0 до I) и t (от 0 до t), находим ln (I /I0) = –Rt/L, или

В момент замыкания (t=0) сила тока I = 0 и u = –ξ . Значит, интегрируя по u и (от –ξ до IR–ξ) и t (от 0 до t), найдем ln[(IR–ξ)]/(–ξ) = -t/τ, или