1 вопрос

Электрический заряд – это физическая величина, которая определяет интенсивность электромагнитных взаимодействий. Электромагнитные взаимодействия – это взаимодействия между заряженными частицами или телами.

ДИСКРЕТНОСТЬ (прерывность; противопоставляется непрерывности. Напр., дискретное изменение какой-либо величины во времени — изменение, происходящее через некоторые промежутки времени (скачками)

Элементарный заряд – это минимальный заряд, которым обладают все заряженные элементарные частицы. Электрический заряд протона равен по абсолютной величине заряду электрона: е = 1,6021892(46) * 10^-19 Кл

закон сохранения электрического заряда. В замкнутой системе алгебраическая сумма зарядов всех частиц остаётся неизменной: q₁ + q₂ + q₃ + ... + q_n = const где q₁, q₂ и т.д. – заряды частиц.

Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.

Электрическая постоянная (по старой терминологии — диэлектрическая проницаемость вакуума), коэффициент пропорциональности e₀ в Кулона законе, определяющем силу взаимодействия двух покоящихся точечных электрических зарядов. В Международной системе единиц (СИ)    ф/м = (8.85418782 ± 0,00000007) ф./м

2.Вопрос

ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ, электрическое поле неподвижных и не меняющихся со временем электрических зарядов, осуществляющее взаимодействие между ними.  Электростатическое поле характеризуется напряженностью электрического поля Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический заряд помещенный в данную точку поля. 

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, которая действует на пробный единичный положительный заряд, помещенный в эту точку поля:   (1) 

линии напряженности электростатического поля — незамкнутые линии: они начинаются на поверхности положительно заряженных тел (или в бесконечности) (рис. 3, а, б) и оканчиваются на поверхности отрицательно заряженных тел (или в бесконечности).                                    

Ф ормула (80.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности

3 Вопрос

A Fr qE

Работа A, совершаемая  силами   электростатического  взаимодействия при премещении точечного заряда q в  электростатическом   поле , равна уменьшению потенциальной энергии взаимодействия W этого заряда с полем

Потенциал электростатического поля

Тело, которое находится в потенциальном поле сил (а электростатическое поле, как уже известно, является потенциальным), обладает потенциальной энергией, за счет которой силы поля совершают работу.

Интеграл - называется циркуляцией вектора напряженности. Т.о. теорема о циркуляции : циркуляция вектора напряженности электростатического поля равна нулю. Из теоремы о циркуляции следует, что силовые линии не могут быть замкнутыми: они начинаются и кончаются на зарядах или уходят в бесконечность

Э квипотенциальная поверхность — понятие, применимое к любому потенциальному векторному полю, например, к статическомуэлектрическому полю или к ньютоновскому гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала).

Так для потенциала поля системы точечных зарядов Q_1, Q₂, Q_n имеем

где r_i - расстояние от точки поля, обладающей потенциалом , до заряда Q_i.

4. Электростатические силы взаимодействия консервативны ,следовательно, система зарядов обладает потенциальной энергией.

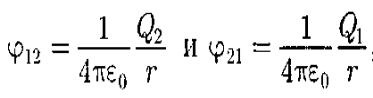
Добавляя к системе из двух зарядов последовательно заряды Q3, Q4,..., можно убедиться в том, что в случае п неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

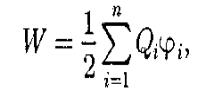где ф, — потенциал, создаваемый в той

точке, где находится заряд Qi, всеми за-

рядами, кроме i-го.

5. Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую х1 — х2 — dх, равна Exdx. Та же работа равна ф1 — ф2 = — dф.Приравниваем,получаем:

Из определения градиента следует, что напряженность Ё поля равна градиенту потенциала со знаком «—«. Знак «—« определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Градие́нт  — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.

6. Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф_Е через эту поверхность.

теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀.  \