Интервальные ряды динамики

Уровни интервального ряда характеризуют результат изучаемого процесса за период времени: производство или реализация продукции ( за год, квартал, месяц и др. периоды), число принятых на работу, число родившихся и.т.п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени.

Средний уровень в интервальных рядах динамики ( ) исчисляется по формуле средней арифметической простой:

• y — уровни ряда (y₁, y₂ ,...,y_n),

• n — число периодов (число уровней ряда).

Моментные ряды динамики

Уровни моментных рядов динамики характеризуют состояние изучаемого явления на определенные моменты времени. Каждый последующий уровень включает в себя полностью или частично предыдущий показатель. Так, например, число работников на 1 апреля 1999 г. полностью или частично включает число работников на 1 марта.

Если сложить эти показатели, то получим повторный счет тех работников, которые работали в течение всего месяца. Полученная сумма экономического содержания не имеет, это расчетный показатель.

В моментных рядах динамики с равными интервалами времени средний уровень ряда исчисляется по формулесредней хронологической:

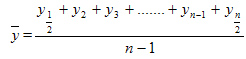
• y -уровни моментного ряда;

• n -число моментов (уровней ряда);

• n — 1 — число периодов времени (лет, кварталов, месяцев).

17. 1. Периодизация развития, т.е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. По существу, это типологическая группировка во времени.

2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета.

3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры, соответственно для стабильных процессов интервалы можно увеличить.

4. Числовые уровни рядов динамики должны быть упорядоченными во времени.  Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.

18) Показатели динамики уровней ряда

Динамика - процесс развития, движения социально-экономических явлений во времени.

Ряды динамики - последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.

Основные элементы рядов динамики:

1) показатель времени - t (определенные даты времени или отдельные периоды);

2) уровни развития изучаемого явления - у.

Уровень рядов динамики - уровень, отражающий

количественную оценку развития во времени изучаемого явления.

Способы выражения уровней рядов динамики:

1) абсолютные величины;

2) относительные величины;

3) средние величины.

Классификация рядов динамики в зависимости от характера изучаемого явления:

1) моментные ряды;

2) интервальные ряды.

Моментные ряды динамики - ряды, отображающие состояние изучаемых явлений на определенные даты (моменты) времени. Суммирование уровней моментного ряда динамики не имеет смысла, так как одни и те же единицы совокупности обычно входят в состав нескольких уровней.

Интервальные ряды динамики - ряды, отображающие итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. В интервальном ряду динамики уровни за примыкающие друг к другу периоды времени можно суммировать, получая итоги (уровни) за более продолжительные периоды.

Полный ряд динамики - ряд, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке.

Неполный ряд динамики - это ряд, в котором уровни зафиксированы в неравностоящие моменты.

Основные случаи несопоставимости рядов динамики:

1) территориальные изменения объекта исследования, к которому относится изучаемый показатель;

2) разновеликие интервалы времени, к которым относится показатель;

3) изменение даты учета;

4) изменение методологии учета или расчета показателя;

5) изменение цен;

6) изменение единиц измерения.

На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.

Периодизации динамики - процесс выделения однородных этапов развития.

Характеристика рядов динамики в зависимости от расстояния между уровнями:

1) с равностоящими уровнями;

2) с неравностоящими уровнями во времени.

Равностоящие ряды динамики - ряды динамики одинаковых периодов, или следующих через равные промежутки времени показателей.

Неравностоящие ряды динамики - ряды с неровными периодами или неравномерными промежутками между датами.

Основное условие правильного построения ряда динамики - сопоставимость всех входящих в него уровней.

Смыкание рядов динамики - объединение в одни ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам.

Условия смыкания рядов; необходимо, чтобы по одному из периодов (переходному) имелись данные, исчисленные по разной методологии (или в разных границах).

18. Статистические характеристики рядов динамики

Классификационный признак	Название ряда динамики	Характеристика ряда динамики
По времени	Моментные	Последовательность (совокупность) уровней, показывающих фактическое наличие изучаемого явления в конкретный момент времени
Интервальные	Последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени*
По форме представления уровней	Ряды абсолютных, относительных и средних величин
По расстоянию между датами или интервалами времени	Полные	Имеют место если даты регистрации или окончания периодов следуют друг за другом с равными интервалами (равноотстоящие ряды динамики)
Неполные	Имеют место, если принцип равных интервалов не соблюдается
По числу показателей	Изолированные	Имеют место, если ведется анализ во времени одного показателя
комплексные (многомерные)	Имеют место, если в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления

19. Индивидуальные индексы и их применение в эконом анализе

Индекс – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различие условий может проявляться во времени (тогда говорят об индексах динамики), в пространстве (территориальные индексы), в выборе в качестве базы сравнения какого-либо условного уровня, например планового показателя, уровня договорных обязательств и т.п. Соответственно вводят индекс выполнения обязательств или, если плановый уровень сравнивается с уровнем предыдущего периода, – индекс планового задания.

В экономическом анализе индексы используются не только для сопоставления уровней изучаемого явления, но главным образом для определения экономической значимости причин, объясняющих абсолютное различие сравниваемых уровней.

Относительная величина, получаемая при сравнении уровней, называется индивидуальным индексом,если исследователь не интересуется структурой изучаемого явления и количественную оценку уровня в данных условиях сравнивает с такой же конкретной величиной уровня этого явления в других условиях

Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например:

Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так, например, получают индекс общего объема товарооборота в агрегатной форме:

При анализе прироста общего объема товарооборота этот прирост также объясняется изменением уровня цен и количества проданных товаров.

Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен I_p, который в предположении первичности изменения количественного показателя (q) и вторичности – качественного (р) имеет вид

Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема I_q , который строится также в предположении первичности изменения количественных показателей (q) и вторичности влияния качественных (р):

В форме мультипликативной индексной модели динамика товарооборота будет выражаться соотношениями

где   

20. Общие индексы в агрегатной форме

Агрегатную форму общего индекса рассмотрим на примере индексного анализа себестоимости продукции растениеводства:

общий индекс затрат на производство продукции (общий индекс товарооборота, общий индексурожайности)

общий индекс себестоимости продукции (общий индекс цен)

общий индекс физического объема (индекс, отражающий динамику товарооборота в сопоставимых ценах)

Количество произведенной продукции и затраты на ее производство

Вид продукции	Выработано продукции,тыс.ц базисный период	Выработано продукции,тыс.ц отчетный период	Себестоимость единицы продукции, руб./ц базисный период	Себестоимость единицы продукции, руб./ц отчетный период
Озимые	4.91	4.28	2.19	4.15
Яровые	1.94	1.16	2.12	8.59
Бобы	1.4	2.66	1.6	9.77

а) общий индекс затрат на производство продукции

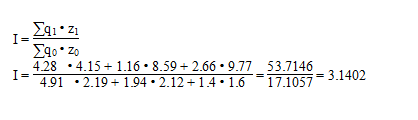
ΔZ = Σq1 • z1 — Σq0 • z0

ΔZ = 53.7146 — 17.1057 = 36.6089 тыс.руб.

За счет всех факторов общие затраты возросли на 214.02% или на 36.6089 тыс. руб.

б) общий индекс себестоимости продукции

ΔZz = Σq1 • z1 — Σq1 • z0

ΔZz = 53.7146 — 16.0884 = 37.63 тыс. руб.

За счет изменения себестоимости общие затраты возросли на 233.87% или на 37.63 тыс. руб.

в) общий индекс физического объема продукции (индекс Ласпейреса)

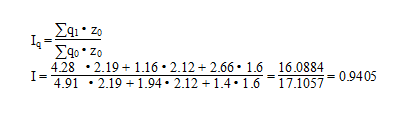
ΔZq = Σq1 • z0 — Σq0 • z0

ΔZq = 16.0884 — 17.1057 = -1.02 тыс.руб.

За счет изменения объема выработанной продукции, общие затраты снизились на 5.95% (100-94,05 или 1-0,9405) или на 1.02 тыс. руб.

37,63-1,02=36,61 тыс.руб.

Покажем взаимосвязь индексов

I  = Iq • Iz = 0.9405 • 3.3387 = 3.1402