Пример решения задачи д5.

Механическая система состоит из ступенчатого шкива 2 (радиусы ступеней R₂ и r₂), груза 1 и сплошного катка 3, прикрепленных к концам нитей, намотанных на ступени шкива (рис. Д5). На шкив при его вращении действует момент сил сопротивления М₂. Массу шкива следует считать равномерно распределенной по внешнему ободу.

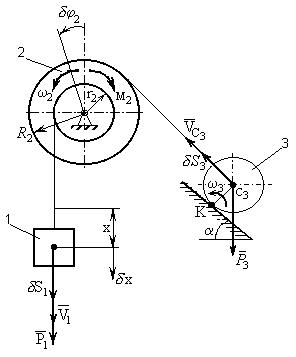
Рис. Д5

Д а н о: R₂ = R; r₂ = 0,5R; P₁ = 8P; P₂ = 4P; P₃ = 6P; M₂ = 0,2PR;  = 30.

О п р е д е л и т ь: а₁ – ускорение груза 1.

Р е ш е н и е

Система имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение х груза 1 (q = x), полагая, что груз движется вниз, и, отсчитывая х в сторону движения, составим уравнение Лагранжа:

= Q. (1)

Определим кинетическую энергию Т системы, равную сумме энергий всех тел:

T = T₁ + T₂ + T₃ . (2)

Так как груз 1 движется поступательно, шкив 2 вращается вокруг неподвижной оси, а каток 3 движется плоскопараллельно, то

(3)

поскольку масса шкива считается распределенной по внешнему ободу, а каток – сплошной (его радиус обозначим r₃), моменты инерции тел 2 и 3 равны:

. (4)

Все скорости, входящие в выражения T₁, T₂ и T₃ , выразим через обобщенную скорость , равную V₁. Если учесть, что V₁ = ₂r₂ , a = = ₂R₂ и что точка К является для катка 3 мгновенным центром скоростей, то получим

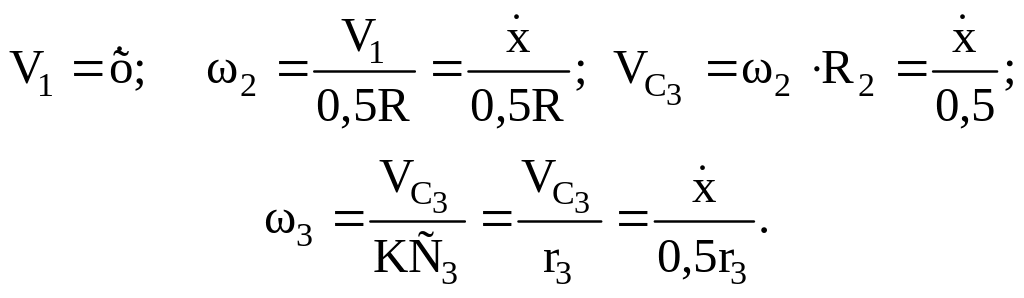₍₅₎

Подставляя величины (5) и (4) в равенства (3), а затем значения T₁, T₂ , T₃ в равенство (2), найдём окончательно, что

T = . (6)

Так как здесь Т зависит только от , то

(7)

Найдём обобщенную силу Q. Для этого изобразим силы, совершающие при движении системы работу, т.е. силы и момент сил сопротивления М₂, направленный против вращения шкива. Затем сообщим системе возможное (элементарное) перемещение, при котором обобщенная координата х получает положительное приращение x, и покажем перемещения каждого из тел; для груза 1 это будет S₁ = x, для шкива 2 – поворот на угол ₂ , для катка 3 – перемещение S₃ его центра. После этого вычислим сумму элементарных работ сил и момента на данных перемещениях.

Получим

Σ A_k = P₁S₁ – M₂₂ – P₃sin S₃ . (8)

Выразим все возможные перемещения через x. Учтя, что зависимости между элементарными перемещениями здесь аналогичны зависимостям (5) между соответствующими скоростями, получим

S₁ = x; ₂ = ; S₃ = R₂  ₂ = . (9)

Подставляя эти значения в равенство (8) и вынося за скобки, найдём, что

Σ A_k = x. (10)

Коэффициент при в полученном выражении и будет обобщенной силой Q.

Следовательно,

Q = P₁ – – 2P₃sin , или Q = 1,6Р. (11)

Подставляя найденные величины (7) и (11) в уравнение (1), получим

60 = 1,6Р.

Отсюда находим искомое ускорение a₁ = .

О т в е т: а₁ = 0,027g.

Примечание. Если в ответе получится а  0 (или   0), то это означает, что система движется не в ту сторону, куда было предположено при решении задачи. Тогда направление момента М против вращения шкива изменится. В этом случае необходимо еще раз составить уравнения (8), (11) и заново определить величину Q.