Пример выполнения задания д-1

Исходные данные: рисунок 1, m=100 кг, β=45°, f=0,25, γ=30°, Р= 120(7,5 + t)Н, х₀=0, =0,5 м/сек, t₁ = 2 сек.

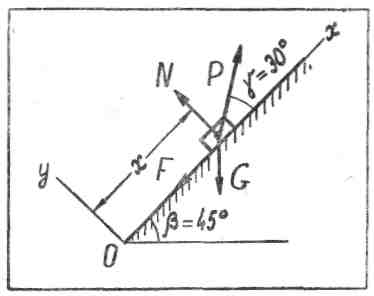
Покажем силы, действующие на тело, рассматриваемое как материальная точка, при его движении по наклонной плоскости.

К телу, кроме заданной силы Р, приложены: сила тяжести G, сила трения F, направленная в сторону, противоположную направлению движения и нормальная реакция плоскости N (рис. 1).

Дифференциальные уравнения движения материальной точки имеют вид:

Учитывая, что в данном случае y=0 = const, у=0,

Сила трения F = fN. Нормальное давление определим из уравнения (2)

Рисунок 1 Подставляя выражение (3) в уравнение (1), имеем

или

Обозначая

получим дифференциальное уравнение движения в виде

Вычислим значения а и b:

Подставим в дифференциальное уравнение (6) заданную силу Р и значения а и b.

или

Интегрируем дважды дифференциальное уравнение 7

Для определения произвольных постоянных воспользуемся начальными условиями:

при t = 0

По этим условиям из уравнений (8) и (9) находим

С₁= 0,5,

C₂=0

Подставляя C₁ и С₂ в уравнения (8) и (9), получим проекцию скорости на ось х в функции времени

и уравнение движения точки

В заданный момент времени t₁ = 2 сек находим положение точки

Проекция скорости точки на ось х в тот же момент

Модуль скорости v =|х₁|=3,38 м/сек.

Задание д-2. Теорема об изменении количества движения материальной точки

У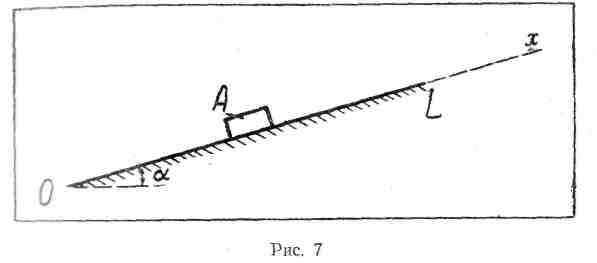 словие задания. На тело А, движущееся по плоскости OL, действует сила Р направленная по оси х. Масса тела — т. Зная закон изменения силы с течением времени и учитывая трение скольжения, определить скорость тела в моменты времени t₃ и t , и проверить полученный результат для момента времени t₁ с помощью дифференциального уравнения движения тела.

Рисунок 2

Тело А принять за материальную точку. Начальная скорость тела v₀ = ₀ (рис. 2). Необходимые данные для решения задачи помещены в табл. 2. При построении графика изменения силы Р с течением времени зависимость P = f(t) между расчетными значениями времени t считать линейной. Значение силы Р, задаваемой в таблице в виде дроби, указывает на то, что модуль силы в заданный момент времени претерпевает «скачок» — в числителе указан модуль силы в конце промежутка времени, а в знаменателе — в начале следующего промежутка времени.

Пример выполнения задания

Дано: m = 40 кг, v₀=10 м/сек, t₁ = 3 сек, t₂ = 8 сек, t₃=15 сек, Р₀ = 0, P₁ = 300 н, Р₂=350/200 н, P₃ = 350 н, α = 30°, f = 0,1.

Покажем силы, приложенные к телу: вес , нормальную реакцию плоскости N¯, силу трения скольжения ¯F и силу ¯Р (рис. Д3). Строим график P=f(t) по заданным значениям P₀, P₁, Р₂ и Р₃ (рис. 4).

Таблица Д2 – Исходные данные к задаче 2

Последняя цифра шифра	Масса тела m,кг	Нчальная скорость м/с	Расчетные моменты времени, сек			Предпоследняя цифра шифра	Значение силы в различные моменты времени, Н				α, град	Коэффициент трения скольжения, ƒ
1	2	3	4	5	6	7	8	9	10	11	12	13
1	35	3.4	4	10	18	1	100	200	150	250	25	0.1
2	20	0	6	10	15	2	200	160	160	120	37	0.25
3	16	5	4	10	16	3	200	200/120	120	0	21	0.1
4	10	0	5	10	16	4	0	180	40	100	32	0.4
5	20	1.5	4	8	12	5	120	120/0	0	160	24	0.08
6	40	3	5	12	16	6	400	300	300	0	40	0.06
7	30	2	6	15	18	7	0	300	0	0	25	0.2
8	50	0	4	6	10	8	75	125	0	0	23	0.12
9	15	1.	5	10	15	9	100	120	0	0	20	0.20
0	45	2	6	12	18	0	0	300	200	200	27	0.1

1. Для определения скорости тела в момент времени t₃ воспользуемся теоремой об изменении количества движения материальной точки в проекциях на ось х.

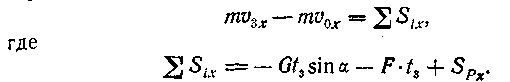
Рисунок 3

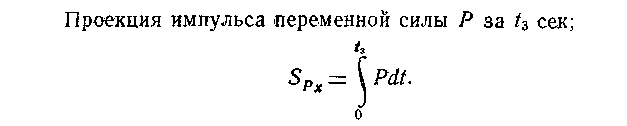
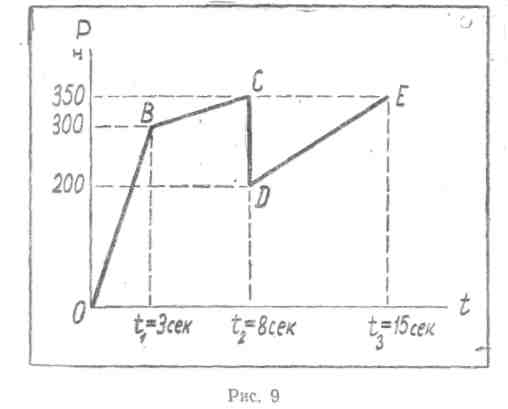
Рисунок 4

Этот интеграл определяется как площадь многоугольника ОВСДЕК на графике P=f(t)

Учитывая, что сила трения скольжения F =f N = f G cos α= = f m g cos α, получаем

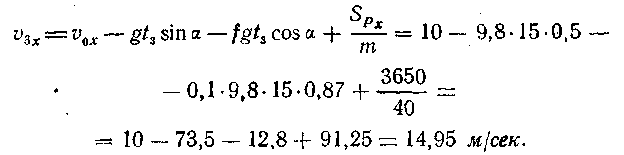
2. Для определения скорости тела в момент времени t₁ поступаем аналогично

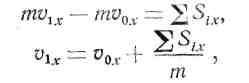
откуда

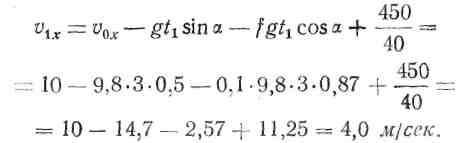
Итак, v_1x = v_t1=3c = 4,0 м/с.

3. Проверим полученный результат с помощью дифференциального уравнения движения материальной точки

Интегрируя полученное дифференциальное уравнение, получаем

При t = 0 = v₀ = 10 м/с. Следовательно, С=10.

Итак,

= 10 - 9,8 (0,5 + 0,1-0,87) 3 + = 4,0 м/сек.