Министерство образования и науки Российской Федерации

Дальневосточный федеральный университет

Школа естественных наук

Операционное исчисление

для направлений подготовки (бакалавриат): «Математика», «Прикладная математика и информатика», «Математика и компьютерные науки»

Учебно - методическое пособие

Составитель Шепелева Р.П.

Владивосток

Издательский дом Дальневосточного федерального университета

2013

УДК 51

ББК

Операционное исчисление: учебно – методическое пособие / сост. Р.П. Шепелева – Владивосток: Издательский дом Дальневосточного федерального университета, 2013.

В учебно – методическом пособии кратко изложен теоретический материал по операционному исчислению: понятия функций – оригиналов и функций – изображений, свойства изображений, нахождение оригиналов функций – изображений и наоборот, решение дифференциальных уравнений операционным методом. Приведены примеры решения задач по всем вышеперечисленным темам, варианты заданий для самостоятельной работы.

Пособие предназначено для бакалавров направлений: «Математика», «Прикладная математика и информатика», «Математика и компьютерные науки».

УДК

ББК

© Шепелева Р.П., составление

2013

Введение

Данное пособие предназначено для проведения занятий в 3 семестре по курсу «Дифференциальные уравнения» для направлений бакалавриата «Математика», «Прикладная математика и информатика», «Математика и компьютерные науки». В пособии кратко приведена теория по операционному исчислению, понятия функций – оригиналов и функций – изображений, свойства изображений, нахождение оригиналов функций – изображений и наоборот, решение дифференциальных уравнений операционным методом. Приведены примеры решения задач по всем вышеперечисленным темам, варианты заданий для самостоятельной работы.

1. Основные понятия

Определение. Функцией – оригиналом называется любая комплексная функция действительной переменной t, определенная на всей числовой прямой и удовлетворяющая условиям:

1. = 0 при t < 0,

2.существуют постоянные М>0, 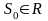такие, что для всех t

< ,

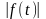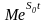3 на любом конечном отрезке [ 0, T] функция может иметь лишь конечное число точек разрыва, притом только первого рода.

Замечание. Число 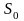называется показателем роста . Для ограниченных оригиналов можно принять = 0.

Простейшей функцией – оригиналом является функция Хевисайда:

Очевидно, что показатель роста функции Хевисайда равен 0.

Определение. Изображением функции – оригинала называют функцию комплексного переменного 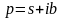, определяемую равенством:

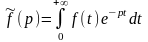. (1)

Теорема. Для любого оригинала изображение f(р) определено в полуплоскости Rep > , где - показатель роста и является в этой полуплоскости аналитической функцией.

Замечание. Функция 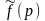, определенная равенством (1), называется также преобразованием Лапласа функции .

Если функция является изображением оригинала , то пишут: 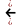. (читается: «функция является оригиналом , или функция является изображением функции ».