§12. Кездейсоқ шаманың орташа мәні. Ықтималдықтардың таралу функциясы

1. Дискретті кездейсоқ шаманың орташа мәні. Егер қандайда бір кездейсоқ Х шамасы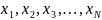 мәндерін қабылдайтын болса, онда осы шаманың орташа мәні былай анықталады:

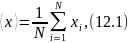
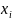шамаларының арасында бірдей мәнге ие болатын шамалар болуы мүмкін, сондықтан (12.1) формуланың оң жағындағы сумма тек қана әртүрлі мәнді шамалары енетіндей қайта топтастыру керек:

мұндағы , ал -(12.1) өрнектегі бірдей мәнге ие бірдей мүшелердің саны. – Х шамасының мәнге ие болу ықтималдығы болса, онда орташа мән үшін жазылған (12.2) формуланы мына түрде жазуға болады:

Осы формула (11.7-формуланы қара) кездейсоқ шаманың математикалық күтілуін ықтималдықты ескеріп анықтайды.

2.Үздіксіз өзгеретін шаманың орташа мәні. Үздіксіз өзгеретін шаманың орташа мәні (12.1) формулаға ұқсас формуламен анықталады. – шамасына тәуелді функция болсын. Онда бұл функцияның мен аралығындағы орташа мәні былай анықталады:

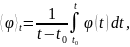
мұнда бұрышты жақша сыртындағы индексі қандай шамаға қатысты функциясының орташа мәні анықталатынын көрсетеді. орташа мәнінің геометриялық түсініктемесі суретте көрсетілген. Функцияның орташа мәні қандай айнымалыға қатысты анықталатындығына тәуелді.

(12.3) өрнекті үздіксіз өзгеретін кездейсоқ шама үшін былай жазуға болады:

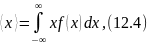
мұндағы 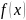– шамасының таралуының ықтималдығының тығыздығы.

3. Дисперсия. Өзгеретін шаманың орташа мәннен ауытқуларын дисперсия сипаттайды. Дисперсия – қарастырылатын шаманың орташа мәннен ауытқуының квадраты ретінде анықталады:

Дисперсияның квадраттық түбірі стандартты немесе орташа квадрат ауытқу деп аталады.

(12.3) және (12.4) формулаларды ескеріп дискретті және үздіксіз өзгеретін кездейсоқ шамалар үшін дисперсияны анықтауға болады. Дискретті кездейсоқ шамалар үшін:

Үздіксіз өзгеретін кездейсоқ шамалар үшін:

4. Ықтималдықтардың таралу функциясы. Кездейсоқ шамасының мәні берілген мәннен аз болуының ықтималдығы, демек 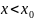, былай анықталады:

мұндағы 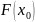функциясы ықтималдықтардың таралу функциясы деп аталады.

Үздіксіз өзгеретін шама үшінықтималдықтардың таралу функциясы -ықтималдықтың тығыздығы арқылы былай анықталады:

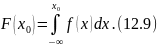
Осы (12.9) өрнектен - функциясы үшін мынадай өрнек аламыз:

Формуланы пайдаланып енетін өрнектерді қайта жазуға болады. Мысалы,

Бақылау сұрақтары:

1. Ықтималдықтар теориясында оқиға дегеніміз не?

2. Сынақ дегеніміз не?

3. Қандай оқиғаны айқын оқиға деп атаймыз?

4. Қандай оқиғаны кездейсоқ оқиға деп атаймыз? Мысалдар келтіріңіз.

5. Қандай оқиғалар сәйкес емес оқиғалар деп аталады?

§13. Жүйенің макроскопиялық және микроскопиялық күйлері

1. Жүйе ұғымы. Құрамында зерттеу нысандары бар кеңістіктің шекті аймағын жүйе деп атаймыз. Жүйенің шекарасы материалдық болуы (ыдыстың қабырғасы) немесе кеңістікте ойша алынуы мүмкін және қозғалмайтын немесе қозғалатын болуы мүмкін. Шекара арқылы зат және энергия тасымалдануы немесе тасымалданбауы мүмкін. Кейде шекара арқылы энергияның кейбір түрі тасымалдануы мүмкін болады. Жүйе тек шекараның ерекшеліктерімен ғана емес, сонымен қатар оның ішіндегі заттың физикалық және химиялық қасиеттерімен де сипатталады. Жүйенің түрі қарастырылатын құбылысқа және қойылған мәселенің шарттарына байланысты таңдалады. Идеал газ да осындай жүйе болып табылады.

2. Макроскопиялық күй. көлемде идеал газ болсын. Газ бөлшектерінің ыдыс қабырғаларымен соқтығысулары абсолют серпімді, ал ыдыстың массасы өте көп болсын, сонда бөлшектердің ыдыс қабырғасымен соқтығысулары нәтижесінде олардың қозғалыстарының күйі өзгермейді. Осындай жағдайда көлемдегі газ ыдыс сыртындағы материалдық денелермен энергия алмаспайды, демек, оқшауланған болады. Осы шарттар орындалса ыдыс ішіндегі газ сыртқы әсерлерден оқшауланған болады және газ ішінде не болса да ішкі себептер нәтижесінде орын алады. Ыдыс ішіндегі газға жеткілікті уақыт аралығында ешқандай сыртқы әсерлер болмаса, онда газдың күйі стационар болып уақыт бойынша өзгермейді. Демек, осы «жеткілікті уақыт аралығында» жүйенің құрамдас бөліктерінде газдың бастапқы қысымдары, температуралары қандай мәндерге ие болса да теңесіп, газ уақыт бойынша өзгермейтін стационар күйге келеді. Сонымен, «жеткілікті уақыт аралығы»жүйенің барлық құрамдас бөліктеріндегі температуралар мен қысымдардың теңесу уақыты. Бұл уақытты қарастырылатын газдағы тасымалдау құбылыстарын зерттеу арқылы бағалауға болады. Мысал ретінде қысымның теңесу уақыты сол ортадағы дыбыс жылдамдығымен анықталатынын айта кетуге болады. Егер ыдыстың сызықтық өлшемі болса, онда бұл уақыт аралығы қатынасымен анықталады. Ауа үшін дыбыс жылдамдығы екенін ескерсек, онда ыдыс өлшемі болғанда жеткілікті уақыт аралығы шамамен секунд болады. Әрине, бұл уақыт макроскопиялық көзқарастан өте аз сияқты, бірақ микроскопиялық көзқарастан өте ұзақ уақыт. Мысалы, ауа молекулалары қалыпты жағдайда 1 секунд ішінде басқа молекулалармен 10⁹ соқтығысулар жасайды. Қысым, температура және көлеммен сипатталатын газ күйін газдың макроскопиялық күйі деп атаймыз.

3. Тепе-тең күй. Сыртқы ортадан оқшауланған көлемдегі газдың стационар макроскопиялық күйі тепе-тең күй болып табылады. Бұл кезде газдың макроскопиялық сипаттамалары болып табылатын қысымы, температурасы және көлемі уақыт бойынша өздерінің тұрақты мәндерін сақтап қалады. Қысым мен температура көлемнің барлық құрамдас бөліктерінде бірдей мәнге ие болуы керек. Жүйенің күйінің тепе-тең екендігін анықтағанда оның оқшауланған болуының маңызы зор. Егер жүйе оқшауланбаған болса, онда жүйе тепе-тең емес стационар күйде болады. Мысалы, газы бар ыдыстың әртүрлі бөліктері сыртқы жылу көздерінен әртүрлі тұрақты температураларда қыздырылып тұрса, онда жүйеде стационар күй орнауы мүмкін. Бірақ мұндай стационар күй тепе-тең күй болмайды. Себебі, ыдыстың бөліктеріндегі қысымдар бірдей болғанымен, температуралары әртүрлі.

4. Микроскопиялық күй.Газдың күйін толық сипаттау үшін оның барлық бөлшектерінің кеңістіктегі орындары мен жылдамдықтарын білу керек. Газ бөлшектерін i=1,2,…,Nиндекстерімен белгілейік, демек қарастырылатын көлемде Nбөлшек болсын. Егер ыдыс көлемі болса, онда қалыпты жағдайдабөлшектер саны 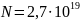болады. Барлық бөлшектерінің кеңістіктегі орындарымен және жылдамдықтарымен сипатталатын газ күйі микроскопиялық деп аталады. Газдың микроскопиялық күйі 6Nсанымен сипатталады,демек, 3N барлық бөлшектердің координаттарымен және олардың 3Nжылдамдықтарының компонентерімен. Бұл шамалар кездейсоқ шамалар болып табылады.

Жүйенің макроскопиялық күйі үш шамамен – қысым, температура және көлеммен сипатталады. Бұл параметрлер жүйенің стационар күйінде тұрақты болады. Алайда газ бөлшектері стационар күйде де үнемі қозғалыста болғандықтан, оның микроскопиялық күйі үздіксіз өзгеріп отырады. Осылай жүйенің бір макроскопиялық күйіне көптеген микроскопиялық күйлер сәйкес келеді. Басқаша айтқанда, берілген бір макроскопиялық күй көптеген микроскопиялық күйлер арқылы жүзеге асырылады. Статистикалық физиканың негізгі мәселесі жүйенің микроскопиялық күйлерімен макроскопиялық күйлерінің арасындағы байланысты зерттеу болып табылады.

5. Жүйелердің статистикалық ансамблі. Жүйелер ансамблі әдісін статистикалық физика сұрақтарын талдағанда қолдану өте ыңғайлы. Көлемдері бірдей болатын Nыдыстар берілсін. Ыдыстардың әрқайсысының ішінде бірдей n бөлшектер болсын. Ішінде зат (газ) бөлшектері бар ыдыс статистикалық жүйе деп аталады. Осындай бірдей статистикалық жүйелер жиынтығы статистикалық ансамбль деп аталады.

Бізді бөлшектердің қалай қозғалатындығы, бастапқы уақыт мезетіндегі олардың сәйкес ыдыстардың қай бөлігінде орналасатындығы қызықтырмайды. Мәселе жеткілікті уақыт аралығынан соң ансамблдің жеке жүйелеріндегі микро және макрокүйлерді зерттеу болып табылады. Сонымен бірдей макроскопиялық күй ансамблдің әртүрлі микрокүйлердегі көптеген жүйелерінде іске асады.

6. Микроканондық ансамбль.Микроканондық ансамбль энергиялары тең оқшауланған бірдей жүйелерден тұрады. Ансамблдер әдісін 1902 жылы американдық физик Гиббс енгізген.

Бақылау сұрақтары:

1. Ықтималдықтар теориясында оқиға дегеніміз не?

2. Сынақ дегеніміз не?

3. Қандай оқиғаны айқын оқиға деп атаймыз?

4. Қандай оқиғаны кездейсоқ оқиға деп атаймыз? Мысалдар келтіріңіз.

5. Қандай оқиғалар сәйкес емес оқиғалар деп аталады?