§11. Ықтималдықтар теориясынан қысқаша түсінік

1. Молекулалық көзқарастан термодинамикадағы барлық физикалық шамалардың орташа мәндерінің мағынасы орындалады. Мұндай шамаларды статистикалық деп атайды. Математикалық көзқарастан статистикалық заңдылықтарды ықтималдықтар теориясы зерттейді.

2.Қазіргі заманғы ықтималдықтың математикалық теориясы абстрактты аксиомалық ғылым ретінде құрылған. Ықтималдық деп бірнеше аксиомалар жүйесіне бағынатын сандарды айтамыз. Абстракциялық теорияда ықтималдықтың нақты мағынасына көңіл бөлінбейді. Ал физикада ықтималдықты нақты процеспен және физикалық шамалармен байланыстырады.

3.Оқиға, сынақ, айқын, кездейсоқ және мүмкін емес оқиғалар.Ықтималдықтар теориясында оқиға немесе жағдай деп орындалуы немесе орындалмауы туралы айтуға болатын барлық құбылыстарды айтамыз. Ықтималдықтар теориясында қандай да бір оқиғаның орындалуын немесе орындалмауын бақылау үшін қойылған тәжірибе сынақ деп аталады.

Егер берілген жағдайда оқиға міндетті түрде орындалатын болса, онда ондай оқиғаны айқын оқиға деп атаймыз, ал оқиға міндетті түрде орындалмайтын болса – мүмкін емес оқиға деп атаймыз.

Егер сынақ кезінде оқиға орындалуы да, орындалмауы да мүмкін болса, ондай оқиға кездейсоқ оқиға деп аталады. Мысалы, монетаны лақтырғанда екі жағы да түсуі мүмкін. Демек бұл кездейсоқ оқиға.

4.Сәйкес емес және тең ықтималдықты оқиғалар. А және В оқиғаларының қосындысы А немесе В оқиғасының пайда болуынан тұратын оқиға болып табылады. Мысалы, жәшікте қызыл, жасыл және ақ шарлар болса, онда жәшіктен шар алғанда оның түрлі-түсті болуы (қызыл немесе жасыл) мына оқиғалардың қосындысы: 1) қызыл шардың пайда болуы; 2) жасыл шардың пайда болуы. А және В оқиғаларының қосындысы А+В болады.

А және В оқиғаларының көбейтіндісі А және В оқиғаларының бірдей орындалу оқиғасы болып табылады. Мысалы, монета екі рет лақтырылғанда бірінші аверс жағынан одан кейін екінші реверс жағының түсуі екі оқиғаның көбейтіндісі: 1)1-лақтырғанда аверс түсуі; 2)2-лақтырғанда – реверс. А және В оқиғасының көбейтіндісі А·В деп белгіленеді.

оқиғаларының бірі сынақ кезінде міндетті түрде орындалса, онда бұл оқиғалар дара мүмкін оқиғалар деп аталады. Осы барлық дара мүмкін оқиғалардың қосындысы айқын оқиға болып табылады.

Егер оқиғаларының бірі орындалғанда, басқалары орындалмайтын болса, онда ондай оқиғалар сәйкес емес оқиғалар деп аталады. Барлық сәйкес емес оқиғалардың көбейтіндісі мүмкін емес оқиға болады.

Егер сынақ кезінде екі кездейсоқ оқиғаның бірінің көбірек орындалуын күтуге ешқандай негіз жоқ болса, онда бұл оқиғалар тең мүмкіндікті немесе тең ықтималдықты оқиғалар деп аталады. Мысалы, монетаны лақтырғанда аверс немесе реверс жағының түсуітең ықтималды.

5.Ықтималдықтың анықтамасы.Кездейсоқ оқиғаның ықтималдығы оның пайда болуының күтілетін мүмкіндігінің сандық өлшемі. Бұл өлшемді енгізу үшін біз дара мүмкін, сәйкес емес, тең мүмкіндікті n-оқиғаны қарастырайық. Әр оқиғаның ықтималдығы деп 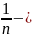бөлшегін айтамыз. Егер жәшікте бірдей нөмірленген 100 шар болса, онда нөмірі 1-ші шарды алу ықтималдығы болады.

Енді осы оқиғалары дара мүмкін, сәйкес емес және тең мүмкіндікті емес оқиғалар болсын.Осы оқиғаларды тең мүмкіндікті оқиғалардың қосындысы түрінде көрсетугеболатын жағдайды қарастырайық. Мысалы, оқиғасы 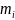дара мүмкін, сәйкес емес, тең мүмкіндікті оқиғалар қатарына жайылсын: оқиғалары дара мүмкін, сәйкес емес және тең мүмкіндікті болады. оқиғасының ықтималдығы

(11.1)

оқиғасы орын алатын оқиғалар , үшін қолайлы жағдайдеп аталады.

Онда ықтималдықтың анықтамасын былай тұжырымдауға болады. Ықтималдықдеп бірдей мүмкін оқиғалар санының сынақ кезінде кездесуі мүмкін барлық мүмкін оқиғалар санына қатынасын айтамыз.

Айқын және мүмкін емес оқиғаларды кездейсоқ оқиғалардың шекті жағдайлары деп қарастыруға болады. Айқын оқиғалардың ықтималдығы 1-ге тең, ал мүмкін емес оқиғалардың ықтималдығы 0-ге тең.

6. Болжам ықтималдық.Ықтималдықтың анықтамасы бойынша сынаққа дейін оқиғалардың тең мүмкіндікті екендігі туралы айтуға негіз бар (симметриялығы, біртектілігі). Сондай-ақ сынаққа дейін оқиғаларды тең мүмкіндікті оқиғалардың суммасы түрінде қарастыруға болады. Сондықтан осылай анықталған ықтималдықты болжам ықтималдық, демек сынаққа дейін ақ анықталған ықтималдық деп атаймыз.

7.Ықтималдықтарды қосу теоремасы.Егер тек қана ықтималдықтың анықтамасын қолданған болсақ, онда әрбір нақты жағдайда оқиғаларды тең мүмкіндікті оқиғаларға жіктеп отыру керек болады. Мұндай қажеттіліктерді ықтималдықтарды қосу және көбейту теоремалары қанағаттандырады. Демек, әр нақты жағдай үшін тең мүмкіндікті оқиғаларды жіктеп отырудың қажеті жоқ.

Сәйкес емес оқиғалардың қосындысының ықтитмалдығы, сол оқиғалардың ықтималдықтарының қосындысына тең. Ықтималдықтың анықтамасын енгізгендегідей дара мүмкін және сәйкес емес оқиғаларды тең мүмкіндікті оқиғаларға жіктейік. В оқиғасы 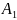және оқиғаларының қосындысы болсын, демек немесе оқиғасының орындалуынан тұрсын. және оқиғалары сәйкес емес болғандықтан В оқиғасына қолайлы тең мүмкіндікті жағдайлардың саны және оқиғаларына қолайлы тең мүмкіндікті жағдайлар суммасына, демек - ге тең. В оқиғасының ықтималдығы:

Сонымен, және оқиғалары сәйкес емес болса, онда

(11.2)

Мысалы, жәшік ішінде 25 қызыл шар, 45 жасыл шар және 30 ақ шар болсын. Онда жәшіктен қызыл шар шығуының ықтималдығы 25/100, ал жасыл шар шығуының ықтитмалдығы 45/100 болады. жәшіктен түсті шар шығуының ықтималдығы

Барлық дербес мүмкін және сәйкес емес оқиғалардың ықтималдығы 1-тең:

(11.3)

(3) өрнек көбіне ықтималдықтың нормирлену шарты деп аталады.

Егер дербес мүмкін сәйкес емес оқиғалар саны екеу болса, онда оқиғалар қарама қарсы деп аталады. Демек, әрбір оқиғаға қарама қарсы оқиға болады. Оның бірі орындалғанда екіншісі орындалмайды.

8. Ықтималдықтарды көбейту теоремасы. А және В оқиғаларының көбейтіндісі олардың бірінің ықтималдығы Р(А), 1-ші оқиға орындалған сияқты есептелген екіншісінің ықтималдығына көбейтіндісіне тең.

А оқиғасы орындалды деп есептеп анықталған В оқиғасының ықтималдығын В оқиғасының шартты ықтималдығыдеп атайды. Р(В/А). Сонымен,

Р(АВ)=Р(А) Р(В/А) (11.4)

Осыны дәлелдеу үшін бізге сәйкес емес және тең мүмкіндікті n оқиға берілсін

Осылардың ішінде алғашқы mоқиға А оқиғасына қолайлы болсын. Осылардың ішіндегі m жағдайда

алғашқы 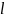жағдай В жағдайына қолайлы болсын, ал қалғандары В оқиғасына қолайлы емес. Демек, А және В оқиғаларына қолайлы жағдайлар саны , сондықтан , 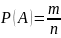. А оқиғасы орындалғандықтан қалған оқиғалары мүмкін емес, ал қалған 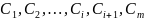жағдайлары тең мүмкіндікті болып қалады. Сондықтан . Сонымен

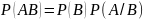(11.5)

Статистикалық тәуелсіз А және В оқиғаларының көбейтіндісінің ықтималдығы олардың әрқайсысының ықтималдықтарының көбейтіндісіне тең:

9.Орташа мән және математикалық күтілу.Қандай да бір «а» шамасы бірдей жағдайда N рет өлшенсін. ретөлшегендегі мәні , рет өлшегенде – , ..., ретөлшегенде– 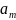болсын. Сондықтан . Олай болса, өлшенген шаманың орташа мәні былай анықталады:

(11.6)

Мұндағы , , 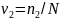…, сәйкес оқиғалардың орындалу жиілігі болып табылады. Өлшеулер кезінде осы нәтижелерден басқа нәтижелер болмасын, демек, бұл мәндердің әрқайсысы дара мүмкін, сәйкес емес болсын. Онда өлшеулер саны N көбейгенде оқиғалардың жиіліктері өздерінің шекті мәндері ықтималдықтарына яғни оқиғаларының пайда болу ықтималдықтарына айналады. (1) - өрнек бұл кезде былай өзгереді:

(11.7)

Осы сумманың мәні М(а)ашамасының математикалық күтілуідеп аталады.

Бақылау сұрақтары:

1. Ықтималдықтар теориясында оқиға дегеніміз не?

2. Сынақ дегеніміз не?

3. Қандай оқиғаны айқын оқиға деп атаймыз?

4. Қандай оқиғаны кездейсоқ оқиға деп атаймыз? Мысалдар келтіріңіз.

5. Қандай оқиғалар сәйкес емес оқиғалар деп аталады?

6. Ықтималдықтың анықтамасын тұжырымдаңыз.

7. Ықтималдықтарды қосу және көбейту теоремаларын тұжырымдаңыз.

8. Ықтималдықтың нормирлену шартын түсіндіріңіз.

9. Математикалық күтілу дегеніміз не?