§8. Орташа квадраттық жылдамдық

1.5-параграфта қысым үшін қорытылып шығарылған формулалар газ молекулаларыныңжылулық қозғалыстарының жылдамдықтары туралы айтуға мүмкіндік береді. Газдағы барлық молекулалар бірдей жылдамдықтармен қозғалмайды. Газ ішінде өте баяу молекулалармен қатар жылдамдықтары орташа жылдамдықтан бірнеше есе үлкен молекулалар да кездеседі. Енді газ молекулаларының орташа квадраттық жылдамдығын қарастырайық. Орташа квадраттық жылдамдық былай анықталады:

яғни молекулалардың ілгерілемелі қозғалысының жылдамдықтарының квадраттарының орташа мәнінің квадраттық түбірі болады. Орташа квадраттық жылдамдықты анықтау үшін мына түрдегі қысым формуласын қарастырайық:

.

Бұдан 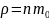, екендігін ескерсек, онда орташа квадраттық теңдеуді мына түрде жаза аламыз:

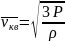(8.1)

Газ тығыздығын былай өрнектеп, орташа квадраттық жылдамдықты Менделеев-Клапейрон теңдеуін қолданып жазааламыз:

.

Осы формуланы қолданып кейбір газдардың молекулаларының орташа квадраттық жылдамдықтарын есептеп көрейік. Мысалы, (273.15 K) температурадағы молекулалық сутегі газының молекулаларының орташа квадраттық жылдамдығын анықтайық. Сутегі молекуласының мольдік массасы .

.

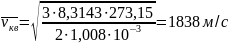Осы жолмен азот молекулаларының орташа квадраттық жылдамдығын және оттегі үшін екендігін анықтауға болады.

2. Штерн тәжірибесі. Молекулалар және атомдар шоғымен жасалған тәжірибелерде де олардың жылдамдығының мәні шамамен -формуласымен есептегендей шығады. Жоғары вакуумдағы молекулалар бір-бірімен соғтығыспайды деп есептеуге болады, олар тек ыдыстың қабырғаларымен соқтығысады. Осыны пайдаланып молекулалар мен атомдар шоғын алуға болады. Молекулалар мен атомдар шоғын жоғары вакуумде металдарды немесе басқа заттарды қыздыру арқылы алады. Шоғырдағы атомдардың жылдамдығын тікелей өлшеуді ең алғаш 1920 жылы О.Штерн іске асырды. Оның классикалық саналатын тәжірибесінің қарапайым сызбасы 8–суретте көрсетілген. Сыртынан күмістің жұқа қабаты жағылған А платина қыл сым С цилиндрдің өсі бойымен орналасқан. Цилиндр ішіндегі ауа шамасы қысымға вакуумдық сорғышпен үнемі сорылып отырған. Қылсым бойымен электр тогы өткенде, ол күмістің балқу температурасынан (961,9 ºС) жоғары температураға дейін қызады. Жоғары температураға дейін қызған күміс интенсивті буланып, оның атомдары түзу сызықты бірқалыпты А қыл сымынан С цилиндрдің ішкі бетіне қарай ұшқан. Күміс атомдары цилиндр бетінде жақсы конденсирленуі үшін цилиндр суытылды. Ұшқан атомдардың жолында жіңішке саңлауы бар В экран қойылды. Атомдар шоғы цилиндрдің ішкі бетіне орнатылған қабылдаушы пластинаға конденсирленді. Цилиндрді және онымен бірге экранмен қылсымды 2500÷2700 мин^-1жиілігімен айналдыруға болады. Осы жүйе тыныштықта болғанда күміс атомдары В саңлауынан өтеді және қабылдаушы пластина бетінде конденсирленіп оның бетінде В саңлауының к ескіні D жазықтығы түрінде құрайды. D жазықтығы А қыл сымымен және В саңлауымен бір жазықтықта жатады. Осыдан кейін жүйені айналдырғанда Саңлаудың кескіні D^/ орынына ығысады. Қабылдаушы пластинаның майысқан бетіндегі D және D^/ кескіндерінің арақашықтығын s әріпімен белгілейік. Бұл арақашықтық 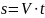формуласымен анықталады, мұнда 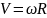-айналған цилиндр бетінің нүктелерінің сызықтық жылдамдығы, R-оның радиусы, -бұрыштық жылдамдығы,t – шамасы күміс атомдарының BD-арақашықтығын өту уақыты. Бұл арақашықтықты l-әріпімен белгілесек, онда , мұнда -күміс атомдарының жылдамдығы. Сонымен, , бұдан күміс атомдарының жылдамдығын мына түрде анықтаймыз:

Штерннің тәжірибелерінде Dкескіні үнемі айқын, ал D^/ кескіні көмескілеу болған. Бұл факт күміс атомдарының жылдамдықтары әртүрлі болғанын көрсетеді. Бұл тәжірибеде қыл сымның температурасы шамамен 1200 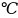болған. Күміс атомдарының жылдамдықтарының мәндері 560÷640 м/с аралығында, демек (8.1) теңдеумен күміс атомдары үшінесептелген орташа квадрат жылдамдық мәніне (584 м/с) өте жақсы жуықтайды. Сонымен, Штерн тәжірибесінің нәтижелері молекула-кинетикалық теориямен сапалық деңгейде үйлеседі.