§42. Нернст теоремасы
Нернст теоремасының тұжырымдамасы. 1906 жылы Нернст эмпирикалық жолмен жаңа іргелі термодинамикалық заң ашты. Бұл заң Нернстің жылулық теоремасы деп аталады. Нернст теоремасы термодинамика бастамаларынан логикалық қорытылмайды, сондықтан бұл теореманы термодинамиканың үшінші бастамасы деп те атайды. Нернст теоремасының тұжырымын Планк берген нұсқасында қарастырайық. Нернст теоремасының мазмұны негізінен екі қорытындыдан тұрады. Бірінші қорытындысына сәйкес жүйенің температурасы абсолюттік нөлге жақындағанда оның энтропиясы соңғы нақты шекке ұмтылады. Демек, дененің абсолюттік нөл температурадағы энтропиясы туралы айтуға болады. Энтропияның термодинамикалық анықтамасына сәйкес
(42.1)
интегралы жүйені бастапқы күйден соңғы
күйге квазистатикалық өткізетін кез
келген жолмен алынады. Интегралда
температура бөлшектің бөлімінде тұр.
Сондықтан температура нөлге ұмтылғанда
(
)
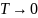интегралдың нақты мәнге ие болатындығы
айқын емес, бәрі абсолюттік нөл температура
аймағында
-дің
қалай өзгеретіндігіне байланысты.
Нернст теоремасының бірінші бөлігі осы
интегралдың нақты мәнге ие болуын талап
етеді.
Нернст теоремасының екінші бөліміне сәйкес абсолюттік нөл температурада жүйені бір тепе тең күйден екінші тепе тең күйге өткізетін барлық процестер кезінде жүйе энтропиясы өзгермейді. Бұдан (42.1) интегралының ұмтылатын шегінің мәні температура нөлге ұмтылғанда ( ) жүйе қандай соңғы күйге келетіндігіне тәуелді емес.
Нернст
теоремасының осы екі бөлімін біріктіріп
былай тұжырымдауға болады. Жүйенің
температурасы абсолюттік нөлге
жақындағанда энтропияның өсімшесі
жүйенің күйін сипаттайтын барлық
параметрлердің (мысалы, көлемге, қысымға,
агрегаттық күйге) мәндеріне тәуелсіз
нақты шекке ұмтылады.
Нернст теоремасы жүйенің тек термодинамикалық тепе-тең күйлері үшін орындалады. Тепе теңсіз және метастабильді күйлер үшін орындалмайды. Егер тепе теңдіктегі жүйенің абсолюттік нөл температурадағы энтропиясын нөлге тең деген шарт орындалса, онда энтропияны анықтаудағы қиыншылықтар жойылар еді. Осылай анықталған энтропия абсолюттік энтропия деп аталады. Осы жағдай үшін Нернст теоремасын былай тұжырымдауға болады. Абсолюттік нөлге жақындағанда жүйенің абсолюттік энтропиясы жүйені сипаттайтын параметрлердің мәндеріне тәуелсіз нөлге ұмтылады. Жүйе энтропиясының өрнегіндегі аддитивтік тұрақтыны осылай анықтау тек еркін жасалған келісім болып табылады. Нернст теоремасының мазмұны аддитивті тұрақтыны таңдаумен байланысты емес.
2. Нернст теоремасының түсіндірмесі. Абсолюттік нөл температураға жету мүмкін емес, сондықтан Нернст теоремасының дұрыстығы туралы тек заттың абсолюттік нөл температурасына жақын температурадағы заттың сипаттамаларының өзгерісіне қарап айтуға болады. Нернст теоремасын больцман формуласымен, демек энтропияның ықтималдылық бойынша интерпретациясына сүйеніп түсіндіруге болады. Ол үшін жүйенің абсолюттік нөл температурадағы күйінің статистикалық салмағын табу керек. Бұл жерде классикалық әдіс жарамсыз болады. Себебі классикалық механика абсолюттік нөл температурада да жүйенің үздіксіз көптеген динамикалық күйлері болатындығын көрсетеді. Кванттық күй деп жүйенің жалпы күйін қарастырамыз, ал жүйенің өзі тұйықталған болуы керек. Абсолюттік нөл температурада жүйенің күйі минимал. Жүйенің мүмкін болатын кванттық күйлерінің саны минимал энергия деңгейі туындалған болмаса бірге тең, ал бұл деңгей туындалған болса бүтін сан болатын туындалу еселігіне тең болады. Осы санмен жүйенің статистикалық салмағы да өрнектеледі. Сондықтан Больцман формуласы бойынша энтропия мәні шекті мәнге тең болады. Осылай Нернст теоремасының бірінші жартысын түсіндіруге болады.
Енді теореманың екінші жартысын түсіндіріп көрейік. Жүйенің көлемі, қысымы сияқты сыртқы параметрлер өзгергенде жүйенің осы күйдегі кванттық күйі энергиясы өзгереді. Еселі деңгейлер аздап немесе толығымен жәй деңгейлерге айналады. Жәй деңгейлер бір еселі деңгейге бірігуі мүмкін. Алайда жәй деңгейлердің жалпы саны тұрақты болып қалады. Егер жүйе термодинамикалық тепе теңдікте болса, онда абсолюттік нөл температурада жүйе ең төменгі энергиялық деңгейде болады және жүйе үшін басқа энергиялық деңгейлер мүмкін емес. Егер сыртқы параметрлер өзгергенде деңгейдің еселігі өзгермесе, онда статистикалық салмағы да өзгермейді, сонымен қатар жүйенің энтропиясы да өзгеріссіз қалады. Бұл талап Нернст теоремасының екінші жартысы. Егер нөлдік деңгейдің еселігі өзгеретін болса, онда жүйенің энтропиясы да ескермеуге болатындай өте аз шамаға өзгереді.