§36. Температураның термодинамикалық шкаласы
1.1848
жылы Вильям Томсон (Лорд Кельвин) Карно
теоремасын қолданып, термометрлік
дененің (заттың) қасиеттерінің
ерекшеліктеріне және термометрдің
құрылымына тәуелді емес рационалды
температуралық шкала құруға болатынын
көрсетті. Карно теоремасы бойынша Карно
циклінің ПӘК-і тек қыздырғышпен суытқыштың
температураларына тәуелді. Қандай да
бір термометрмен өлшенген қыздырғыш
пен суытқыштың эмпирикалық температураларын
және
деп белгілейік. Онда
(36.1)
мұндағы
- таңдалған
және
эмпирикалық температуралардың универсал
функциясы.Бұл функцияның түрі Карно
машинасының құрылымына және жұмыстық
денесіне тәуелді емес.
2.Температураның термодинамикалық шкаласын құру үшін және температураларының қарапайым функциясын қарастырамыз:
.
(36.2)
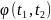
-функциясы
-функциясы
арқылы оңай сипатталады.
-функциясының
жалпы түрін анықтайық. Ол үшін
температуралары тұрақты үш жылулық
резервуарды қарастырайық. Бұл
резервуарлардың эмпирикалық
темпера-тураларын сәйкесінше
және
деп белгілейік. Осы резервуаларды
суытқыш және қыздырғыш ретінде қолданып
үш Карно циклін жүргіземіз (29-сурет).
және
температуралары 1-2,
4-3, 6-5
изотермаларына сәйкес келсін.1-2-3-4
және 4-3-5-6
Карно циклдері үшін
функциясын былай анықтауға болады:
,
.
Осы екі теңдеуді бірге шешсек, онда:
.
Біз 1-2-5-6 Карно циклін сипаттайтын өрнекті алдық. Демек, 1-2-3-4 және 4-3-5-6 Карно циклдері 1-2-5-6 циклін береді. Себебі, бұл екі циклде біз 4-3 изотермасын оң және теріс бағыттарда өттік, сондықтан бұл изотерманы қарастырмауға болады. Сонымен,
.
Соңғы екі өрнекті салыстырсақ,
,
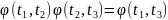(36.3)
бұдан
,
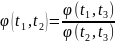(36.4)
немесе
.
(36.5)
Бұл
қатынас
аргументінің кез келген мәні үшін дұрыс
болады. Себебі теңдіктің сол жағы
температурасына тәуелді емес. Егер
аргументін тұрақты етіп тағайындасақ,
онда
функциясын
функциясымен
алмастыра аламыз.
функциясы сәйкесінше
функциясымен
алмастырылады. Олай болса,
(36.6)
Сонымен
функциясы
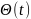функциясының
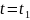және
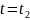болғандағы мәндерінің қатынасы болып
табылады.
шамасы тек қана температураға тәуелді
болғандықтан, оны дененің температурасының
өлшемі ретінде қабылдауға болады.
шамасын абсолюттік термодинамикалық
температура деп атайды.
3.
қатынасын эксперимент жүзінде анықтауға
болады. Ол үшін
және
жылу мөлшерлерін өлшеу қажет, алайда
жылу мөлшерлерінің қатынасы
және
температураларын бір мәнді анықтамайды.
Себебі,
функциясы
параметріне тәуелді, ал (36.6) өрнегі
параметріне тәуелді емес.
параметрінің таңдалған мәніне қарай
термодинамикалық температуралардың
мәні де әртүрлі болады. Термодинамикалық
температураны бірмәнді анықтаудың екі
жолы бар:
Біріншіден,
қандай да бір екі температуралық нүктені
аламыз. Мысалы, мұздың балқуының қалыпты
нүктесі және судың қайнауының қалыпты
нүктесі. Бұл температуралық нүктелерді
және
деп, ал оларға сәйкес Карно цикліндегі
жылу мөлшерлерін
және
деп белгілейміз. Сондай-ақ,
екі
температура айырымын 100 градусқа тең
деп қабылдаймыз. Сонымен, екі температуралық
нүкте арасындағы интервал теңдей 100
бөлікке бөлінеді және оның әрқайсысы
1 Кельвинге тең. Енді (36.6) қатынасын мына
түрде жазамыз:
,
(36.7)
Бұл
қатынастардан
қатынасын экспериментте өлшеу арқылы
және
температураларын анықтауға болады.
Нақты тәжірибелерде бұл қатынас
өлшенбеген, бірақ бөгде өлшеулер
нәтижесінде
және
температуралары былай анықталған:
,
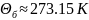.(36.8)
Кез келген дененің температурасын мынадай формула бойынша анықтауға болады:
,
(36.9)
Ол үшін дене мен еріп жатқан мұз арасында Карно циклін жүргізіп және жылу мөлшерлерін өлшеу керек. Осылай құрылған шкала температураның абсолюттік термодинамикалық шкаласы деп аталады.Бұл бізге белгілі (§3) екі реперлік нүкте бойынша температура шкаласын жасау әдісі болып табылады.
Екіншіден, температуралық шкаланы бір ғана реперлік нүкте бойынша, яғни бір температуралық нүкте бойынша жасауға болады. Мұндай нүкте ретінде судың үштік нүктесін алуға болады. Себебі, судың қалыпты қайнау температурасын 0,002-0,01 ºС дәлдігімен, мұздың қалыпты балқу температурасын 0,0002-0,001 ºС дәлдігімен қайталауға болады, ал судың үштік нүктесін арнайы құралдар көмегімен 0,0001 ºС дәлдігімен өлшеуге болады. Осыларды ескеріп 1954 ж. «Өлшемдер бойынша 10-шы генералдық конференцияның» шешімі бойынша температураның абсолюттік термодинамикалық шкаласын бір реперлік нүкте бойынша, дәлірек айтқанда судың үштік нүктесі бойынша жасау бекітілген. Сондай-ақ, үштік нүктенің температурасының мәні 273,16 К деп анықталған.
Бақылау сұрақтары:
Вильям Томсонның (Лорд Кельвин) термодинамикалық температура шкаласын жасау принципін түсіндіріңіз.
Термодинамикалық температура шкаласын жасауда неліктен судың үштік нүктесі алынған?
Судың қалыпты қайнау және мұздың қалыпты балқу температуралары қандай дәлдікпен анықталады?