Вузли. Характеристика сімейства базових функцій.
На рис. 4 всі базові функції мають однакову форму і розміщені на рівних відстанях один від одного. Це дуже симетрично і елегантно, але насправді бажано варіювати довжини інтервалів таким чином, щоб певні контрольні точки впливали на значно більший сегмент кривої, а певні - на менший. Це створює умова для неоднорідності (Non - Uniform) в описі кривої.
Однак визначення послідовності точок, на які розбивається вісь параметра t, є не дуже легким завданням. Адже при зміні відносних інтервалів між такими точками, випадає можливість міняти тривалість впливу контрольних точок на рухому вздовж кривої частинку.
Точки, що розмежовують інтервали, отримали назву вузлів (knots), а їх впорядкований список - назва вузлового вектору (knot vector).
Вузловий вектор базової функції, представлений на рис. 12.11, має вигляд:
{ 0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0 }
Це приклад однорідного вузлового вектору (uniform knot vector), в якому всі функції визначені на однакових часових інтервалах.
Рис.
5. Приклад однорідного
вузлового вектору
Наступний рисунок (рис. 6) являє приклад кривої, створеної на основі такого вузлового вектору.
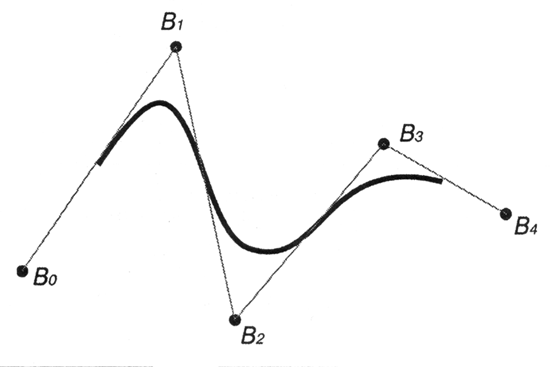Рис.
6. NURBS-крива з однорідним
вузловим вектором
Якщо змінити вузловий вектор, наприклад, таким чином:
{0.0, 1.0, 2.0, 3.75, 4.0, 4.25, 6.0, 7.0}
То вийде інше безліч неоднорідних (non-uniform) базових функцій (рис. 7) і, відповідно, інша форма кривої (рис. 8), яка будується на тих же контрольних точках, що й на рис. 6.
Рис.
7. Неоднорідні базові
функції для множини контрольних точок
Рис.
8. NURBS-крива с неоднорідним
вузловим вектором
Характеристика сімейства базових функцій
Для будь-якого значення параметра t сума всіх базових функцій, як ми пам’ятаємо із властивостей, строго дорівнює 1.
Якщо ваги всіх контрольних точок позитивні, крива лежить в області, отриманої з'єднанням крайніх (зовнішніх) контрольних точок. Такий "габаритний" контейнер отримав назву "опуклої оболонки" (convex hull).
Раціональні криві
Звернемося до ключової букві в назві NURBS - "R", що означає "rational" (раціональний). Раціональні криві, порівняно із звичайними (нераціональними - "non - rational") В- сплайнами, володіють двома додатковими і дуже важливими властивостями:
вони забезпечують коректний результат при проекційних трансформаціях (наприклад, масштабуванні), а нераціональні В-сплайни - тільки при афінних (відображення площини або простору в себе, при якому прямі переходять у прямі) трансформаціях (наприклад, переміщеннях);
їх можна використовувати для моделювання кривих будь-якого виду, включаючи конічні перетини (окружності, еліпси, параболи і гіперболи).
Ці властивості (до речі, вельми значні) досягаються за рахунок чотиривимірного уявлення звичайної тривимірної контрольної точки { х, у, z }. Це означає, що кожна контрольна точка представляється чотирма координатами { х, у, z, w }. Остання координата w означає вагу (weight) контрольної точки, про який вже згадувалося раніше (згадаймо приклад з гравітацією або холодильником).
Спочатку координата w дорівнює одиниці, але при збільшенні цього значення для контрольної точки збільшується ступінь її впливу на форму кривої і остання сильніше вигинається в бік контрольної точки (рис. 9).
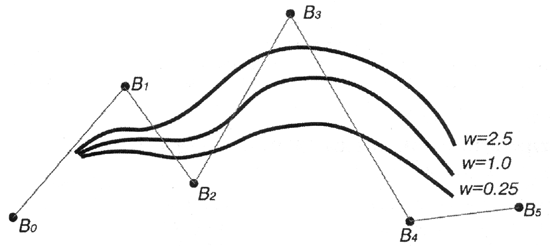Рис.
9. Зміна форми кривої
при зміни ваги контрольної точки
Зауваження
Важливо зауважити, що істотним є тільки відносну зміну ваг контрольних точок. Якщо вдвічі збільшити ваги всіх контрольних точок, то форма кривої не зміниться.
Приклад
Квадратична (другого ступеня) NURBS-крива визначається трьома контрольними точками (рис. 10). У всіх трьох кривих вузловий вектор має вигляд:
{0.0, 0.0, 0.0, 1.0, 1.0, 1.0}
Ваги першої та останньої контрольних точок у кожної кривої рівні 1. Якщо вага центральної вершини менше 1, то результуюча крива являє собою сегмент еліпса (рис. 10, а). Якщо її вага дорівнює 1, утворюється парабола (рис. 10, б). Якщо ж її вага набагато більше 1, то крива перетвориться в гіперболу (рис. 10, в).
Рис.
10. NURBS-криві з різними
вагами центральної контрольної точки