11. Теорема Бернулли для газов.

Газ, находящийся в покое, производит давление на поверхность всех тел, с которыми он соприкасается. Давление это направлено перпендикулярно поверхности и называется статическим давлением. Статическое давление, согласно известному закону Паскаля, во всех точках одного и того же горизонтального слоя одинаково. Удары молекул газа производят внешнее давление, а их взаимные соударения - внутреннее.

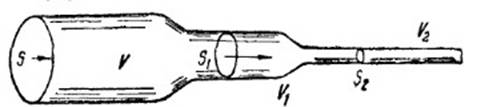
Распределение давлений в струе подчиняется закону, открытому Д. Бернулли. Представим себе струю газа, протекающего по трубе переменного сечения. Причиной движения газа является его первоначальное давление, под действием которого газ устремляется в трубу и приобретает известную скорость. Когда поток газа установится, то через все сечения трубы в единицу времени будет протекать один и тот же объем газа, равный произведению площади поперечного сечения струи S на ее скорость V:

SV=S₁V₁=S₂V₂

Скорости струй в различных сечениях будут неодинаковы: чем меньше площадь поперечного сечения струи, тем больше скорость, и наоборот.Также при изменении скорости струи изменяется и ее давление.

Сжатый газ производит работу. Запас работы, или энергия газа, прямо пропорционален давлению. Движущийся газ так же обладает некоторым запасом кинетической энергии. Кинетическая энергия газа = скоростной напор = , выражение показывает, какую работу (в килограммометрах) способен произвести 1 м³ воздуха при полной его остановке.

В струе переменного сечения газ имеет наименьшее давление там, где он движется с наибольшей скоростью, а наибольшее — где скорость его наименьшая. Это заключение представляет собой содержание теоремы Бернулли.

В механике доказывается, что для всех сечений струи

где р и р₁ означают давление воздуха для двух разных сечений струи, cкоростные напоры для тех же сечений.

Это уравнение показывает нам:

что сумма энергии давления и скоростного напора (кинетической энергии) есть величина постоянная (const) для всех сечении струи; что разность давлений р и p₁ в различных сечениях равна разности в скоростных напорах; что для нахождения разности давлений р и р₁ в мерах, принятых аэродинамикой, т. е. в кг/м² и при отыскании скоростных напоров необходимо подставлять в уравнение значения V в м/сек и массовую плотность ρ в кг·сек2/м4; что увеличение скоростного напора вызывает уменьшение давления.

11. Основное уравнение Эйлера для турбомашин.

20. Теорема Жуковского о подъемной силе крыла. Механизм образования подъемной силы.

R=-i×ρ×V_∞×Г – определяет общую теорему Жуковского о подъемной силе крыла (в бизвихревом плоскопараллельном потоке идеальной несжимаемой жидкости). При циркуляционном обтекании возникает поперечная сила. При безотрывном обтекании кругового цилиндра поступательным потоком жидкости при наличии вращающегося цилиндра возникает подъемная сила, равная произведению плотности жидкости, скорости и циркуляции. Подъемная сила – перпендикулярна к направлению вектора скорости.

Величина циркуляции определяется циркуляцией вертикальной и горизонтальной составляющей вектора скорости:

Доказательство теоремы Жуковского.

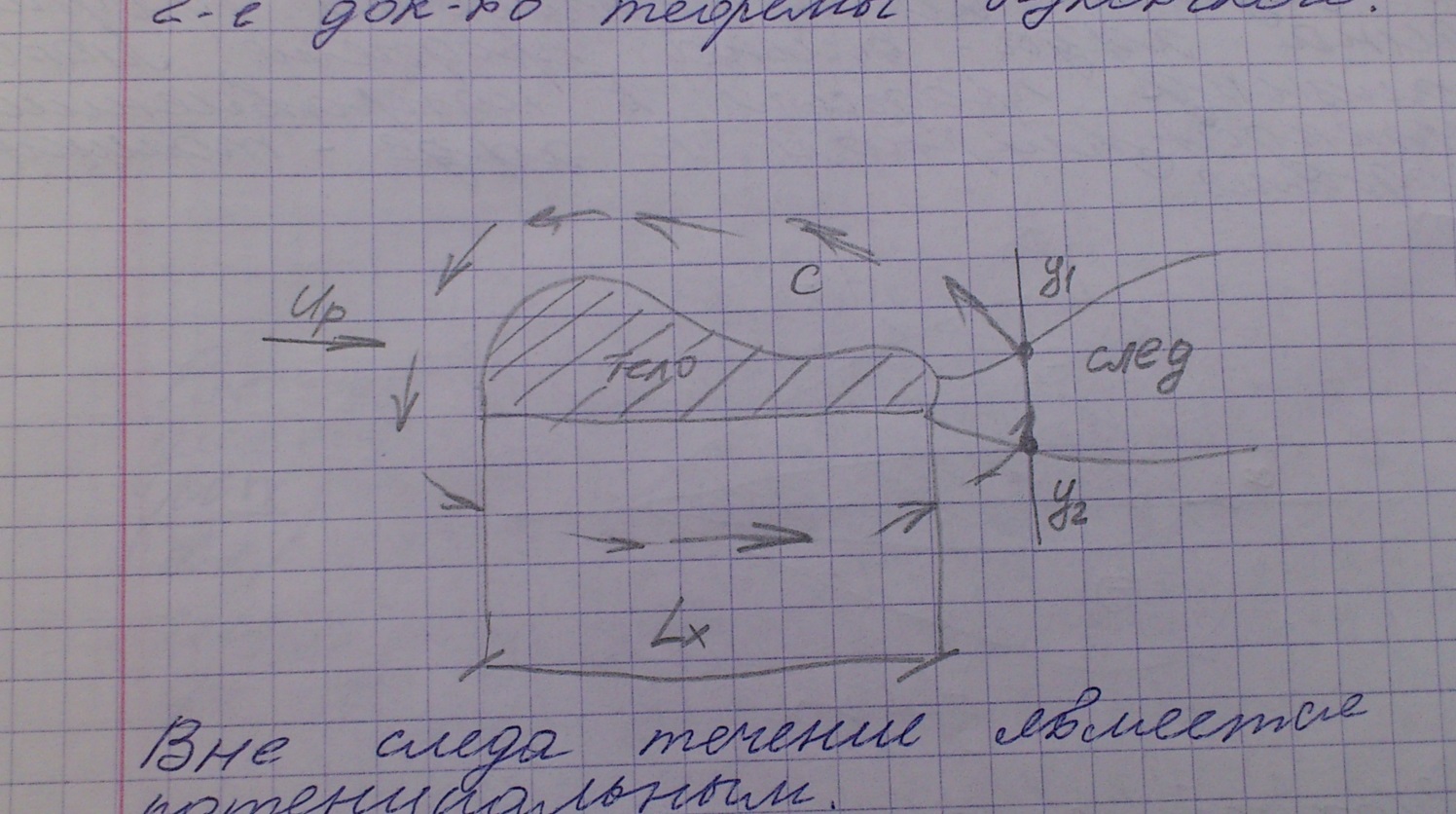
Вне следа течение является потенциальным. Чем шире след, тем больше циркуляция.

Подъемная сила:

F_y=-ρ×U×∫Гdz.

Циркуляция: Г=-2Ul∑A_nsin(nθ).

Для крыльев большого размаха Су = const (l>l_x).

Угол атаки – угол между вектором скорости набегающего потока на бесконечности и направлением хорды.

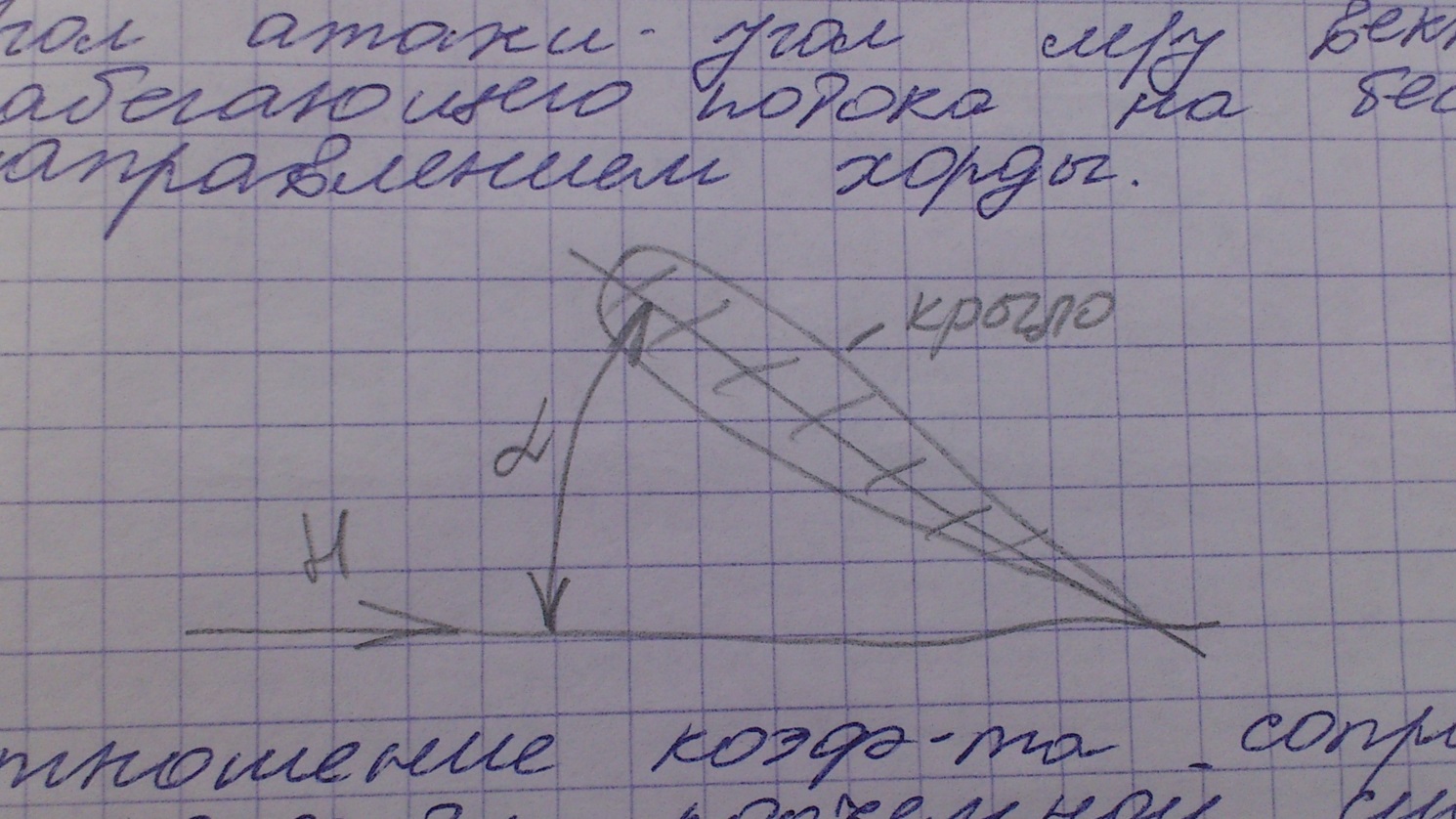
Отношение коэффициента сопротивления С_х к коэффициенту подъемной силы называется аэродинамическим качеством. Лучшая аэродинамика тела достигается при 0<α<10⁰. В пределах отношения С_х/С_у =20…100 – крыло хорошо обтекаемо, нет отрыва потока.

21. Прямой скачок уплотнения. Соотношение скоростей до и после скачка.

Механизм образования скачков. При движении тела с большой скоростью впереди него образуется пространство с повышенным давлением среды, которое вызывает сопротивление движению тела. Повышенное давление в этой области распространяется с большой скоростью во все стороны в виде волн давления. Основная особенность волн давления заключается в том, что фронт волн очень узок, и поэтому состояние газа изменяется скачком. В связи с этим ударные волны называются скачками уплотнения. 

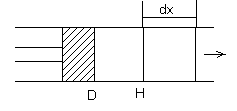
0 Н 1

Под влиянием резкого смещения поршня в трубе перед поршнем возникает и распространяется волна сжатия. За бесконечно малый промежуток времени d фронт волны переместится на расстояние dx. При этом в области H-0 за время d произошло повышение давления от Pн (давление невозмущенного потока) до P1 (давление за фронтом волны). В соответствии с повышением давления произошло и повышение плотности на величину Повышение плотности означает, что из объема 0-H в объем Н-1 перетечет элементарное количество газа: Если фронт ударной волны составляет прямой угол с направлением движения потока, то такая волна называется прямой ударной волной или прямым скачком уплотнения.

Найдем соотношение скоростей газа до скачка V1 и после скачка V2.

Из (1.56)

  (1.60)

из (1.59)

, с учетом (1.57)

   (1.61)

Подставим в (1.61) выражение (1.60)

 (1.62)

Одним из решений (1.62) является случай, когда  , т.е. скачек отсутствует этот случай для нас интереса не представляе т, поэтому сократив (1.62) на   найдем другое решение:

  (1.63)

  (1.63.а)

Из получения зависимости следует, что если поток сверхзвуковой, то после скачка уплотнения скорость в нем становится дозвуковой. Другой вариант трактовки несостоятелен. Если предположим, что изменение скорости обратное, то что это соответствует скачку разряжения существование которого невозможно. Доказательство этой невозможности основано на том, что в скачке разряжения должна уменьшиться энтропия потока, что противоречит второму закону термодинамики.