
- •Квантовая оптика. Квантовая механика
- •Предисловие
- •Методические рекомендации по оформлению задач
- •Основные формулы
- •Примеры решения задач
- •Тема 1. Тепловое излучение Задачи
- •Тема 2. Фотоэффект Задачи
- •Тема 3. Эффект Комптона
- •Примеры решения задач
- •Варианты задач
- •Тема 4. Строение атома
- •Примеры решения задач
- •Варианты задач
- •Тема 5. Длина волны де Бройля
- •Примеры решения задач
- •Варианты задач
- •Тема 6. Соотношение неопределенностей Гейзенберга
- •Примеры решения задач
- •Варианты задач
- •Тестовые задания
- •Литература
- •Приложение
- •Постоянные величины
- •Некоторые приставки единиц измерения
- •Оглавление
- •Квантовая оптика. Квантовая механика
Примеры решения задач
Пример 1. Во сколько раз увеличится мощность излучения абсолютно черного тела, если максимум энергии излучения передвинется от красной границы (λкр = 0,76 мкм) видимого спектра к его фиолетовой границе (λф = 0,38 мкм)?
Дано: λкр = 0,76 мкм = 7,6∙10-7 м ; λф = 0,38 мкм = 3,8∙10-7 м.
Найти: X
= ![]()
Р е ш е н и е
Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, определяется из закона смещения Вина
λmax
=
![]() ,
,
где Т - термодинамическая температура излучателя;
с1= 2,9∙10-3 м·К - постоянная Вина.
По формуле определяем температуру излучателя, соответствующую красной и фиолетовой границам видимой области спектра
Tкр
=
![]() ; Tф
=
; Tф
=
![]() .
.
Мощность излучения абсолютно черного тела
Р = Rэ S,
где Rэ - энергетическая светимость абсолютно черного тела;
S - площадь поверхности излучающего тела.
В соответствии с законом Стефана-Больцмана
Rэ = σT4,
где σ - постоянная Стефана-Больцмана.
Тогда для красной и фиолетовой границ видимой области спектра
Pкр = σT4крS, a Pф = σT4фS.
Следовательно,
X
= ![]() =
=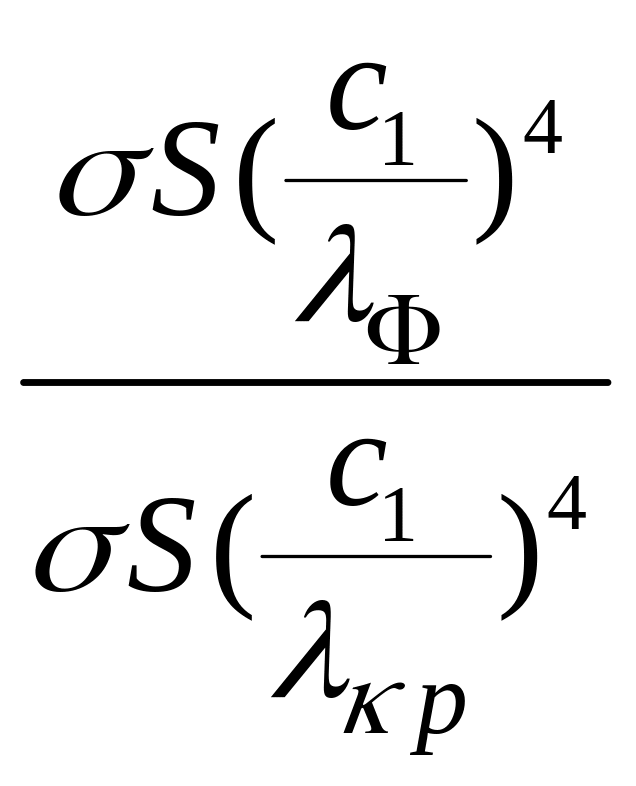 =
(
=
(![]() )4.
)4.
Произведем вычисления
X =
(![]() )4
= 24 = 16.
)4
= 24 = 16.
Ответ. Мощность излучения увеличивается в 16 раз.
Пример 2. Определить с помощью формулы Планка энергетическую светимость ∆Rэ, абсолютно черного тела, приходящуюся на узкий интервал длин волн ∆λ = 10 Ǻ, соответствующий максимуму спектральной плотности энергетической светимости при температуре тела Т= 3000 К.
Дано: ∆λ = 10 Ǻ = 10∙10-10м; Т = 3000 К.
Найти: ∆Rэ.
Р е ш е н и е
Спектральная
плотность энергетической светимости
абсолютно черного тела характеризует
распределение энергии в спектре излучения
тела по длинам волн и выражается формулой
rλ,T
=![]() ,
где dRэ -
энергетическая светимость, приходящаяся
на интервал длин волн от λ до λ+dλ.
,
где dRэ -
энергетическая светимость, приходящаяся
на интервал длин волн от λ до λ+dλ.
Отсюда следует, что
∆![]() =
rλ,T
∙ ∆λ,
=
rλ,T
∙ ∆λ,
где rλ,T
= ![]() ∙
∙  .
.
Используя закон
смещения Вина λ =![]() ,
формулу Планка можно
записать так
,
формулу Планка можно
записать так
rλ,T
=
 =
=
 Т5
Т5
или
rλ,T = с2∙T5.
Эту формулу называют вторым законом Вина.
Константа
с2 =
=
1,36∙10-5 ![]()
вторая постоянная
Вина.
вторая постоянная
Вина.
Тогда расчетная формула ∆ = rλ,T∙∆λ примет упрощенный вид:
∆ = с2∙Т5∙∆λ.
Подставив числовые значения величин, получим
∆
=1,36∙10-5![]() ∙
(3000К)5∙10-9м = 3,2∙103
∙
(3000К)5∙10-9м = 3,2∙103![]() .
.
Ответ: ∆![]() 2.
2.
Пример 3. Давление света с длиной волны 0,55 мкм нормально падающего на зеркальную поверхность равно 9 мкПа. Определить концентрацию фотонов вблизи поверхности.
Дано: λ = 0,55 мкм; р = 9 мкПа; ρ = 1.
Найти: n.
Р е ш е н и е
Давление света при нормальном падении на поверхность с коэффициентом отражения ρ определяется по формуле
р
=![]() (l
+ ρ) = w(l
+ ρ),
(l
+ ρ) = w(l
+ ρ),
где I интенсивность света; с скорость света в вакууме; w объемная плотность энергии излучения, w = I/c.
Объемная плотность энергии w равна произведению концентрации фотонов п (числа фотонов в единице объема) на энергию одного фотона ε = hс/λ, т.е.
W
=![]() ,
,
где h - постоянная Планка; λ - длина волны света.
Подставим энергию в формулу давления
р
=![]() (1+ρ),
(1+ρ),
получим
n
=![]() .
.
Проводя вычисления, найдем
n
= 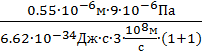 = 1,25∙1013м-3.
= 1,25∙1013м-3.
Ответ: n = 1,25 ∙ 1013 м3.
Пример 4. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найти длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В.
Дано: λк=0,257 мкм; U=1,5 В.
Найти: λ.
Р е ш е н и е
Согласно уравнению Эйнштейна для внешнего фотоэффекта
![]() =
A + Wmax,
(1)
=
A + Wmax,
(1)
где h - постоянная Планка; с - скорость света в вакууме; λ - длина волны света; А - работа выхода электронов из металла; Wmax - максимальная кинетическая энергия фотоэлектронов.
Красная граница фотоэффекта определяется из условия равенства энергии фотона ε = hc/λ работе выхода электронов А, т.е.
![]() = A.
(2)
= A.
(2)
Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов U
Wmax = eU, (3)
где е - элементарный заряд (заряд электрона).
Подставляя выражения (2) и (3) в (1), получим
![]() =
=![]() +eU.
(4)
+eU.
(4)
Из уравнения (4) найдем длину волны света
λ
= (![]() +
+
![]() )-1.
(5)
)-1.
(5)
Подставляя в (5) числовые значения, получим
λ
= (![]() )-1
= 1,96∙10-7м = 0,196мкм
)-1
= 1,96∙10-7м = 0,196мкм
Ответ: λ = 0,196 мкм.
Пример 5. Определить максимальную скорость υmax фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ1= 0,155 мкм; 2) γ-излучением с длиной волны λ2=1 пм.
Дано: 1) λ1= 0,155 мкм = 1,55∙10-7м; 2) λ2 = 1 пм = 1∙10-12м.
Найти : υmax
Р е ш е н и е
Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта
ε = A+Wmax,
где ε
=![]() - энергия фотонов, падающих на поверхность
металла;
- энергия фотонов, падающих на поверхность
металла;
А - работа выхода электрона из металла;
Wmax - максимальная кинетическая энергия фотоэлектронов.
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия фотона много меньше энергии покоя Е0 - электрона, то кинетическую энергию фотоэлектрона можно найти по классической формуле
Wmax
=![]() .
.
если же энергия ε фотона сравнима по величине с энергией покоя Е0 электрона, то кинетическую энергию фотоэлектронов необходимо вычислять по релятивистской формуле
W =
E - E0 =
E0(![]() ),
где 𝛽 =
),
где 𝛽 =![]() .
.
Вычислим энергию фотона ультрафиолетового излучения по формуле
ε1=![]() =
=
![]() Дж
= 1,28∙10-18 Дж,
Дж
= 1,28∙10-18 Дж,
или
ε1
=![]() эВ.
эВ.
Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (Е0 = 0,51 МэВ). Следовательно, кинетическая энергия фотоэлектрона может быть выражена по классической формуле
ε1
= A+![]() ,
откуда υmax =
,
откуда υmax =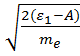 ,
,
где А = 7,5-10 -19 Дж = 4,7 эВ - работа выхода электронов из серебра.
Произведем вычисления
υmax=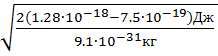 = 1,08∙106
= 1,08∙106![]() .
.
Вычислим энергию фотона γизлучения
ε2
=![]() =
=![]() Дж
= 1,99∙10-13Дж
Дж
= 1,99∙10-13Дж
или ε2
=![]() эВ
= 1,24∙106эВ = 1,24 МэВ.
эВ
= 1,24∙106эВ = 1,24 МэВ.
Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (ε2 = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона:
Wmax= ε2 = 1,24 МэВ.
В данном случае для вычисления скорости фотоэлектрона следует взять релятивистскую формулу кинетической энергии.
Из этой формулы найдем
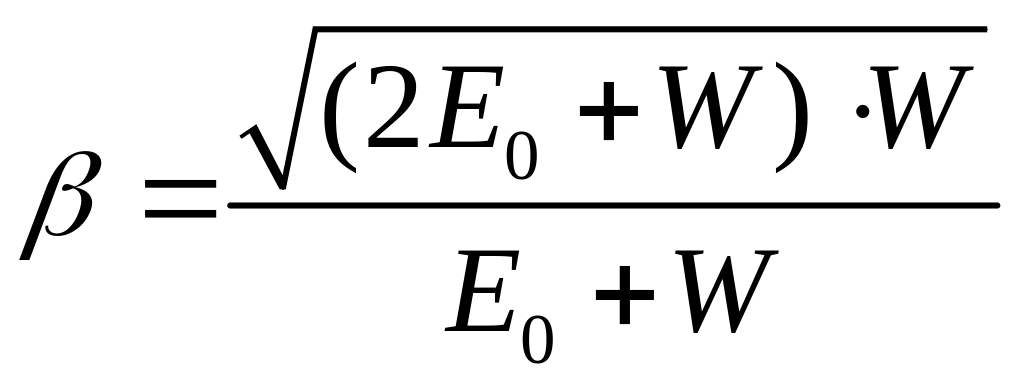 .
.
Заметив, что υ = c∙𝛽 и Wmax = ε2, получим
υmax
= 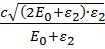 .
.
Проведем вычисления
υmax
= = 2,85·108 м/с.
= 2,85·108 м/с.
Ответ. 1) υmax = 1,08∙106 м/с; 2) υmax = 2,85∙108 м/с.
