7. Замена переменной в неопределенном интеграле

Рассмотрим неопределенный интеграл Положим .

Теорема. Пусть функция имеет непрерывную производную , тогда

Доказательство. Прибегнем к следующему свойству первообразной функции: если – первообразная для , то – первообразная для . Следовательно, согласно определению понятия неопределенного интеграла: или

(1)

Но в силу свойств неопределенного интеграла или (2)

Из равенств (1) и (2) следует, что где разумеется .

Примеры.

1) Линейная подстановка

Если то

Рассмотрим . Положим равносильно равенству . Так как , то согласно теореме о замене переменной в неопределенном интеграле

В частности,

2) Рассмотрим

Положим , тогда и

Так как

3) Рассмотрим – постоянная.

Положим (подстановка Эйлера). То есть и, соответственно,

Так как то

Следовательно,

4) Рассмотрим .

Положим , тогда и

Так как то

5) Рассмотрим неопределенный интеграл вида (в числителе подынтегральной функции стоит производная от знаменателя).

Положим . Тогда и

то есть

В частности,

8. Интегрирование по частям в неопределенном интеграле

Теорема. Если функции и дифференцируемы в рассматриваемом промежутке, то

Доказательство. Согласно правилу дифференцирования произведения функций

Следовательно, и поэтому

.

В силу свойств неопределенного интеграла .

Таким образом

Произвольную постоянную в правой части этого равенства можно опустить, так как неопределенный интеграл содержит в качестве слагаемого произвольную постоянную, а сумма двух произвольных постоянных есть произвольная постоянная.

Теорема доказана.

Так как и , то формулу интегрирования по частям можно представить в виде или краткой записи: .

Примеры.

1) Рассмотрим неопределенный интеграл – натуральное число. В случае положим , , тогда , (произвольную постоянную опускаем) и

(1)

В случае полагаем , тогда, и

(2)

Из равенств (1) и (2) следует, что

(3)

В случае полагаем , тогда , и

(4)

Из равенств (3) и (4) следует, что .

Аналогично можно поступить при

2) Аналогично можно найти и

Например, рассмотрим, Положив , , найдем d и . То есть

Положим теперь , , следовательно и . Так что и потому

3) Рассмотрим неопределенный интеграл вида положим тогда и

Имеем:

Итак, . В частности, для :

4) Рассмотрим неопределенный интеграл .

Положим , , тогда и .

Имеем . Но

Итак,

5) Рассмотрим неопределенный интеграл

Положим , , тогда

Имеем Сделаем замену переменной: Тогда и .

Значит,

Следовательно,

9. Интегрирование рациональных функций

Напомним основные понятия и утверждения, касающиеся рациональных функций.

Определение. Рациональной функцией переменной называется отношение двух многочленов этой переменной: где и – многочлены переменной .

Теорема. Любая рациональная функция с вещественными коэффициентами может быть представлена в виде суммы цело-рациональной функции, (то есть многочлена) и простейших дробно-рациональных функций 1-го и 2-го рода (то есть функций вида , где и – вещественные числа, – натуральное число и , , , – вещественные числа, – натуральное число, причем ).

Согласно этой теореме и свойству линейности неопределенного интеграла, вычисление неопределенного интеграла от рациональной функции с вещественными коэффициентами сводится к вычислению неопределенных интегралов от цело-рациональной функции и от простейших дробно-рациональных функций 1-го рода и 2-го рода.

а) Рассмотрим неопределенный интеграл от цело-рациональной функции

Согласно свойству линейности неопределенного интеграла имеем:

Таким образом, неопределенный интеграл от цело-рациональной функции (многочлена степени ) есть цело-рациональная функция (многочлен степени ).

б) Рассмотрим неопределенный интеграл от простейшей дробно-рациональной функции 1-го рода – натуральное число.

Пусть

Пусть .

в) Рассмотрим неопределенный интеграл от простейшей дробно-рациональной функции 2-го рода: – натуральное, Пусть .

Обозначим: и

Тогда

Рассмотрим

Так как по условию то при .

Поэтому,

Рассмотрим .

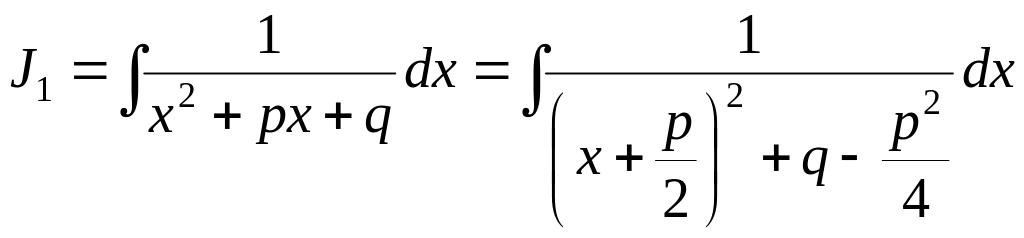Сделаем замену переменной: тогда и

где .

То есть

Итак,

Пусть .

Обозначим и

Тогда

Рассмотрим .

Сделаем замену переменной . Тогда .

Получаем

Итак,

Рассмотрим .

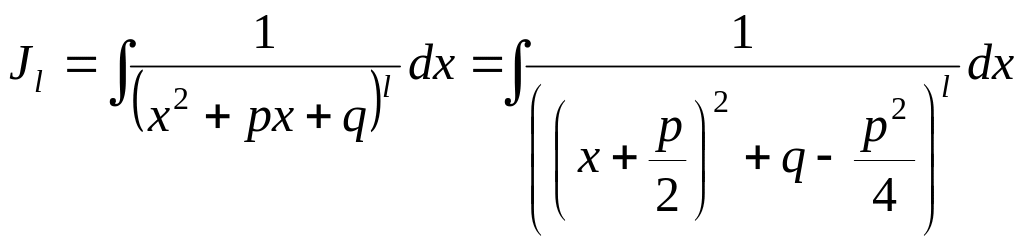Сделав замену переменной и обозначив , получим

Выведем рекуррентную формулу, которая выражает через

Имеем:

Итак, (*)

Рассмотрим

Этот интеграл вычислим методом интегрирования по частям.

Положим ,

Тогда ,

Значит, то есть .

Возвращаясь к равенству (*), получим:

то есть .

Эта рекуррентная формула позволяет свести вычисление неопределенного интеграла к вычислению неопределенного интеграла , который в свою очередь сводится к вычислению интеграла , и так далее до вычисления неопределенного интеграла .

Итак, при где вычисляется по рекуррентной формуле. После вычисления нужно вернуться к переменной , заменив

Пример. Вычислить .

Это неопределенный интеграл от простейшей дробно-рациональной функции 2-го рода, так как

(**)

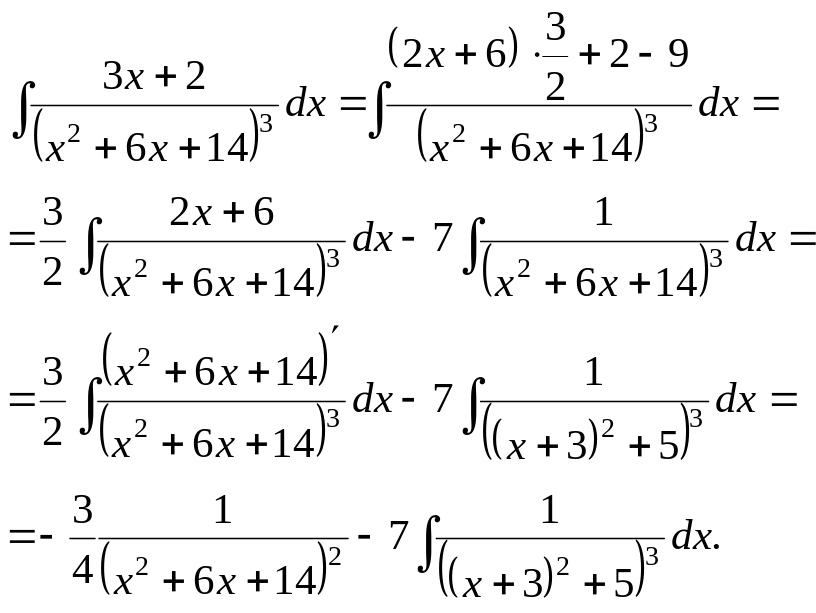Рассмотрим где .

Применим рекуррентную формулу, при :

Для вычисления снова применим рекуррентную формулу, при :

Подставив в предыдущее равенство, получим:

или

где

Таким образом,

Переходя к переменной , получим:

Подставив это выражение в равенство (**) , получим искомый результат.