50. Динамическое действие нагрузок. Прочность материалов при напряжениях, периодически меняющихся во времени.

Быстро изменяющаяся нагрузка вызывает перемещения элементов конструкции с ускорениями, в результате чего возникают инерционные силы, которые необходимо учитывать в расчете. Такие нагрузки, а также вызываемые ими перемещения, деформации и напряжения, называются динамическими.

При расчете конструкций на действие динамических нагрузок используется принцип Даламбера, согласно которому движущуюся с ускорениями систему в каждый момент времени можно рассматривать как находящуюся в состоянии покоя, если к внешним силам, действующим на систему, добавить силы инерции.

Величина d элементарной силы инерции, действующей на бесконечно малый элемент тела, равна произведению его массы dm на ускорение a и направлена в сторону, противоположную ускорению:

,

где dQ b dV – вес и объем бесконечно малого элемента тела, - объемный вес материала, g – ускорение силы тяжести.

При расчете стержней удобно ввести распределенную по длине стержня инерционную нагрузку:

,

Где q= F – вес единицы длины стержня, dV – объем элемента стержня, F(x) – площадь поперечного сечения, dx – длина стержня.

При решении многих задач сопротивления материалов динамические перемещения , деформации и напряжения , возникающие от действия динамической нагрузки , могут быть найдены путем умножения соответствующих статических перемещений, деформаций, напряжений, возникающих от действия статической нагрузки, на так называемый динамический коэффициент

Величина динамического коэффициента зависит от вида нагрузки, геометрических размеров, массы, материала сооружения и ряда других факторов. При проектировании конструкций, работающих под действием переменных (периодических) нагрузок, необходимо уметь прогнозировать их длительную прочность и долговечность.

Рассмотрим пример определения нормальных напряжений в поперечном сечении оси вагона

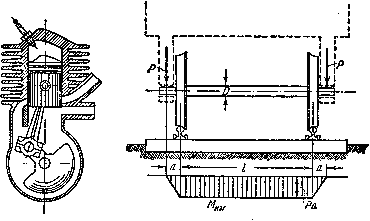
Вес вагона вызывает изгиб оси. Соответствующая расчетная схема и эпюра изгибающих моментов изображены на рисунке.

При вращении оси вагона точка А поперечного сечения оказывается попеременно в зонах растяжения и сжатия. Закон изменения нормальных напряжений в точке А в зависимости от времени t определяется по формуле: ,

Где - момент инерции сечения оси, - угловая скорость вращения.

Таким образом, нормальные напряжения в поперечном сечении оси изменяются по периодическому закону с периодом и амплитудой .

Рис.2. Изменение напряжения в точке А.

 Совокупность всех значений переменных напряжений за один период процесса их изменения называется циклом напряжений.

В рассмотренном случае макс. и минимальное напряжения цикла равны по величине и противоположны по знаку. Такой цикл называется симметричным.

Если к вращающемуся валу , работающему на изгиб, дополнительно приложить постоянную по величине растягивающую (сжимающую) силу N, то напряжения будут изменяться по з-ну:

При этом и напряжения цикла не равны между собой. Такой цикл напряжений называется ассиметричным.

Отношение называется коэффициентом асимметрии цикла. Для симметричного цикла R = -1.

Наибольшее значение максимального напряжения цикла, которое не вызывает разрушения испытываемого на выносливость образца из данного материала принеограниченно большом числе циклов называется пределом выносливости.