39. Расчет стержней и рам на температурные нагрузки и осадку опор

основные положения технической теории расчета плит; основы расчета на динамическую нагрузку и на устойчивость условия для определения основных характеристик ферм и обеспечения их устойчивости; типы сечений элементов решетки ферм.

Определение перемещения сечения стержня плоской статистически определимой стержневой системы при действии температурных воздействий и при смещении ее опор

Температурные перемещения

 Перепишем интеграл Мора (7) из лекции 9 в виде:

   (1)

(см. рис. 3 – 5 лекции 8). Формулой Мора в приведенном виде можно пользоваться для определения перемещений системы, вызванных действием температуры. Если верхнее волокно элемента стержня нагрето на t1, а н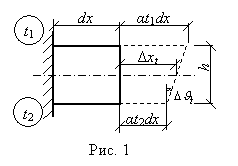 ижнее – на t2 градусов Цельсия, то принимая прямолинейный закон распределения температуры по высоте поперечного сечения, будем иметь (рис. 1) для симметричного поперечного сечения:

,

где α – температурный коэффициент линейного расширения.

 Деформации сдвига в элементе от действия температуры не возникают.

 Подставив найденные значения Δxt и Δ t в выражение (1), получим формулу для нахождения температурных перемещений

   (2)

 Предполагается, что вдоль каждого стержня заданное изменение температуры одинаково и высота h каждого элемента системы постоянна по всей его длине.

 Если стержневая система содержит только прямолинейные или ломаные стержни постоянного сечения, то формула (2) может быть переписана в более простой форме:

   (3) 

где   и    – площади единичных эпюр  и  . Если деформации элемента dx от температуры и от единичной силы аналогичны, то знак соответствующего члена формулы (3) будет положительным, если деформации будут не совпадать, то необходимо брать знак (–).

 Пример 1. Определить горизонтальное перемещение подвижной опоры В при изменении температуры по рис. 2. Высоту поперечного сечения принять h = a /10.

 Строим единичные эпюры   и   (рис. 2, б,в) от приложенной в точке В в направлении искомого перемещения единичной силы Р = 1. Затем определяем площади единичных эпюр:

для ригеля:  = ab/2,  = 1·a = a; для стойки:  = b2/2,  = b2/a.

 Определяем температурные параметры:

для ригеля: t1 = 40о, t2 = 10о; для стойки t1 = 20о, t2 = 10о.

 По формуле (3) находим:

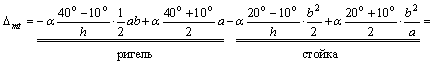= α(–150b – 35b2/a + 25a).

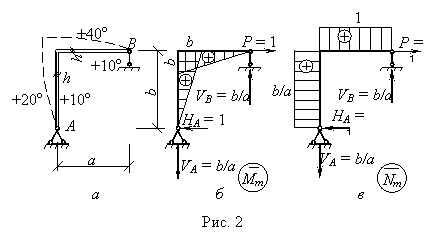Знак (+) нужно поставить перед членом с  , так как изменение температуры вызывает удлинение стойки и ригеля, также как и действие единичной (рис. 2, в). Перед членом с    стоит знак (-), так как температурное воздействие вызывает удлинение внешних волокон ригеля и стойки (рис. 2, а), а изгибающий момент  от действия единичной силы Р = 1, наоборот, вызывает укорочение внешних волокон (рис. 2, б).

 При определении перемещений от действия на сооружение температуры нельзя пренебрегать членом формулы, зависящим от продольной силы.

Определение перемещений от осадки опор

 Осадки опор могут быть случайными (просадки грунта, оползень, размыв грунта) при отсутствии нагрузки на сооружение или могут возникать под действием нагрузки в результате податливости основания.

Перемещения от случайных осадок опор

 Пусть шарнирно подвижная опора рамы, изображенной на рис. 3, а, переместилась вертикально на величину Δ. Определим вертикальное перемещение точки k. Для этого создадим единичное состояние данной системы и в направлении искомого перемещения Δk приложим силу Р = 1 (рис. 3, б). Опорную реакцию, возникающую в том же опорном стержне, переместившимся вертикально на величину Δ, обозначим через R. Составим уравнение равновесия (рис. 3, б):

Σ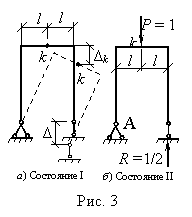 МА = P·l – R·2l = 0,

и находим опорную реакцию R = 1/2.

 На основании теоремы о взаимности работ для двух состояний, показанных на рис. 3, а,б, составим условие: 

W12 = W21, или 0 = (PΔk – R Δ),

откуда находим

Δk = R Δ = Δ/2.

 Работа сил первого состояния на перемещениях второго состояния W12 = 0, так как сил в первом состоянии нет. Второе слагаемое правой части формулы Бетти взято с отрицательным знаком, так как направление силы R и перемещения Δ не совпадают.

 При перемещениях опор статически определимого сооружения по направлениям опорных закреплений внутренние усилия в сооружении не возникают.

 Таким образом, для определения перемещения или угла поворота, возникающего в статически определимом сооружении от смещения его опор в направлении опорных закреплений, необходимо:

выбрать единичное состояние сооружения, считая смещающуюся опору неподвижной,

загрузить сооружение в направлении искомого перемещения единичной силой или моментом,

определить реакции в тех опорных связях единичного состояния, которые по условию задачи смещаются,

составить выражение работы сил единичного состояния на перемещениях действительного и приравнять эту работу нулю,

решить полученное уравнение относительно искомого перемещения.

Перемещения от нагрузки, вызывающей упругие осадки

 Пусть под действием нагрузки q трехшарнирная рама получает равные вертикальные осадки опор Δ = V/ko (рис. 4, а), где ko – коэффициент оседания опоры (или жесткость упругого основания, Н/м, которая численно равна силе, вызывающей единичное смещение). Найдем вертикальное перемещение шарнира С, учитывая только влияние изгибающих моментов МF (рис. 4, б). Приложим единичную силу Р = 1 в шарнире С по направлению искомого перемещения и строим единичную эпюру  (рис. 4, в).

 Применим теорему о взаимности работ (W12 = W21):

откуда находим

41 Понятие об устойчивости и критической силе Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.

Обычно потеря устойчивости системы сопровождается большими перемещениями, воз-никновением пластических деформаций или разрушением. Возможны также случаи, когда система, потеряв устойчивость, переходит в режим незатухающих колебаний. Особая опасность потери устойчивости заключается в том, что она происходит внезапно и при низких значениях напряжений, когда прочность материала еще далеко не исчерпана.При анализе устойчивости конструкций следует различать устойчиво е и неустойчивое равновесие системы.

При устойчивом(шарик в ямке) равновесии тело, выведенное какой-либо силой из своего первоначального положения, воз-вращается в это положение после прекращения действия силы.

При неустойчивом(шарик на горке) равновесии тело, выведенное какой-либо силой из своего первоначального положения, продолжает деформироваться в направлении данного ему отклонения, и, после удаления внешнего воздействия, в исходное состояние не возвращается. В этом случае говорят, что произошла потеря устойчивости. Между этими двумя состояниями существует переходное состояние, называемое критическим, при котором деформированное тело находится в безразличном(шарик на прямой линии) равновесии: оно может сохранить первоначальную форму, но может и потерять ее от самого незначительного возмущения.

Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. С момента наступления критического состояния до момента разрушения деформации системы нарастают крайне быстро, и практически нет времени принять меры по предотвращению грозящей катастрофы. Таким образом, при расчете на устойчивость критическая нагрузка подобна разрушающей при расчете на прочность. При этом условие устойчивости можно записать в следующем виде:

Fmax≤Fкр,

или в напряжениях

σmax ≤ [σу ]= Fкр A.