24. Определение перемещений и углов закручивания стержней круглого сечения интегрируя уравнение

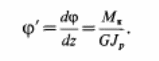
в пределах от 0 до z получим выражение для углов закручивания

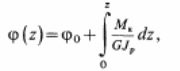где

угол закручивания начального сечения. Если это сечение закреплено, то

. В частном случае когда и , получим

эпюры для этого простого случая изображены на и о рис. 8.1

при наличии распределенной скручивающей нагрузки законы изменени утлов закручивания стержня являются более сложными выведем уравнение, связывающее эти две величины между собой.Продифференцироваввыражение

по z с учетом

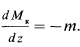, получим

Полученное уравнение можно назвать дифференциальным уравнением утлов закручивания

Из этого уравнения следует например, что на участках стержня с равномерно распределенной нагрузкой углы закручивания изменяются по закону квадратной параболы. после того, ка найдено выражение

по формулам

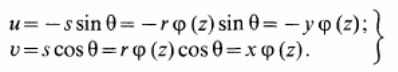
могут быт определены перемещения

Пример 8.2 Построим эпюры для стержня ступенчато постоянного сечения изображенного на рис. 8.12 жесткость участка ВС обозначим через на этом участке действует равномерно распределенная скручивающая нагрузка с интенсивностью m. Пусть жесткость участка АВ равна , и в сечении в действует сосредоточенный момент При построении эпюры удобно начать вычисления со свободного конца, а при построении эпюры с заделки. вычислим сначала значения крутящих моментов на участке

для угла закручивания согласно

и

имеем: на участке АВ

29. Постановка граничных условий в балках

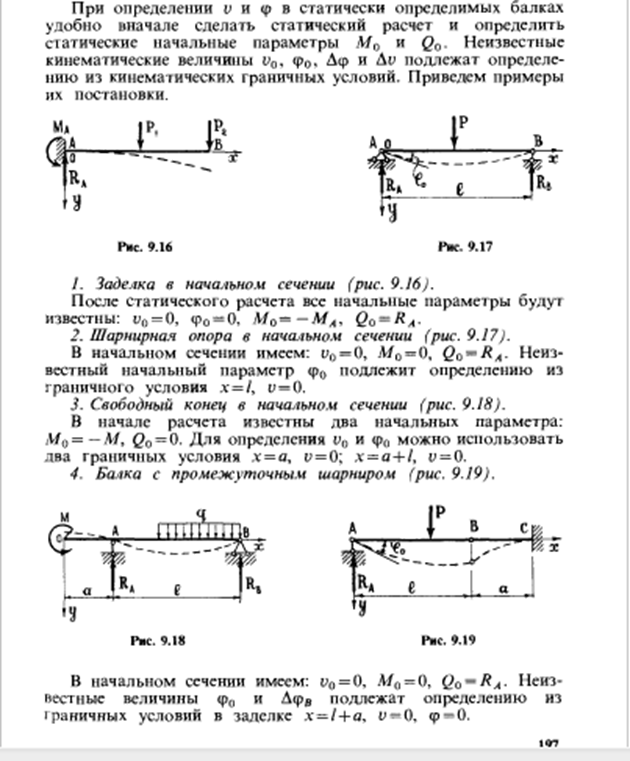
30. Теоремы о взаимности работ и Максвелла — Мора.

   Пользуясь понятием о потенциальной энергии, можно установить следующую зависимость между деформациями в различных сечениях балки. Если к балке, нагруженной силой приложить затем статически силу в сечении 2, то к прогибу точки приложения силы от этой же силы прибавится (Рис.1) прогиб от силы , равный ; первый значок у буквы у указывает точку, для которой вычисляется прогиб; второй — обозначает силу, вызывающую этот прогиб.

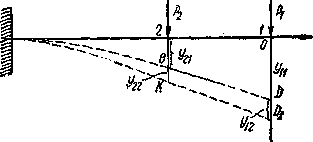Рис.1. Расчетная схема к теореме о взаимности работ

 Полная работа внешних сил составится из трех частей: работы силы на вызванном ею прогибе , т. е. , работы силы на вызванном ею прогибе ее точки приложения , т. е. , наконец, работы силы на прогибе ее точки приложения от силы , т. е. .Таким образом, накопленная в стержне при действии обеих сил энергия будет равна:

 Это количество энергии деформации зависит лишь от конечных значений сил и прогибов и не зависит от порядка нагружения. Если к балке, загруженной силой , приложить затем силу то, повторив цепь вычислений, получим:

Сравнивая оба значения U, получаем:

т. е. работа силы (или первой группы сил) на перемещениях, вызванных силой (второй группой сил), равна работе силы на перемещениях, вызванных силой .

   Это и есть теорема о взаимности работ. Ее можно сформулировать и иначе: работа первой силы ( ) при действии второй ( ) равна работе второй силы при действии первой.

 Теорема Максвелла—Мора.

Прогиб балки в точке приложения сосредоточенной силы Р равен:

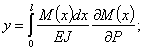аналогичное выражение мы имеем и для угла поворота с заменой производной на . Выясним, что представляют собой эти производные.

   Если на балке расположена какая угодно нагрузка из сосредоточенных сил , , ,..., моментов , ,..., сплошных нагрузок , ..... то момент М(х) в любом сечении такой балки выражается линейной функцией от нагрузок:

Рис.2. Частная расчетная модель метода Максвелла — Мора.

Коэффициенты , ,..., , …, , ... являются функциями пролета балки, расстояний точек приложения сил и моментов от опор и абсциссы х взятого сечения. Пусть мы отыскиваем прогиб точки приложения силы ; тогда

так как , ,..., , ,..., , ..., , ,..., , …, , ... при этом дифференцировании постоянны. Но можно рассматривать как численную величину момента М в любом сечении балки от действия так называемой единичной нагрузки, т. е. силы ; действительно, подставляя в формулу вместо его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем .

Например, для балки, изображенной на Рис2, а, изгибающий момент равен:

   Производная; но это как раз и будет выражение изгибающего момента нашей балки, если мы ее нагрузим силой 1, приложенной в той же точке В, где расположена сила Р (Рис.2, б), и направленной в ту же сторону.

   Аналогично, производная изгибающего момента М (х) по паре сил численно представляет собой изгибающий момент от пары с моментом, равным единице, приложенной в том же сечении, где имеется пара , и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой .Таким образом, для отыскания перемещения (прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента от соответствующей единичной нагрузки, приложенной в сечении, где ищем перемещение ; тогда это перемещение выразится формулой

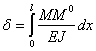
   Эта формула была предложена Максвеллом в 1864 г. и введена в практику расчета О. Мором в 1874 г. Если мы в полученном выражении под подразумеваем прогиб, то момент надо вычислять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице.

Для примера рис.2 имеем:

	(рис.2,а)
	(рис.2, б)

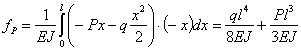
   Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус — наоборот.

   Если при определении изгибающих моментов придется делить балку на участки, то соответственно и интеграл в формуле распадется на сумму интегралов.

   Сравнивая формулу Кастильяно с формулой Мора, нетрудно заметить, что они отличаются лишь одним множителем. В теореме Кастильяно или , в теореме Мора .

   Следовательно, производная от изгибающего момента по обобщенной силе — это то же самое, что изгибающий момент от силы .