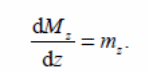21.Упруго-пластический изгиб.
Исследование упруго-пластического изгиба при произвольной зависимости ограничим случаем сечения, имеющего две оси симметрии, которые мы примем за оси Предполагая, что внешние силы приложены в плоскости из условий симметрии заключаем, что в этой же плоскости произойдет и изгиб. Зависимость между в растянутой и сжатой областях одна и та же, поэтому, очевидно, ось является нейтральной осью сечения (ниже это будет проверено).
Сохраняя гипотезу плоских сечений, положим:
Пусть известно, что для материала балки
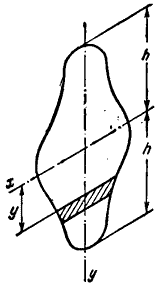
Ширина сечения на расстоянии у от нейтральной оси есть .
Будем считать, что b задано как функция отношения . Элементарный момент сил, действующих на заштрихованную полосу (рис. 155) ширины b и высоты относительно оси х есть
Приравнивая сумму моментов внутренних сил в сечении сумме моментов внешних сил,получим:
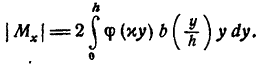
Вследствие симметрии интегрирование от заменено интегрированием от нуля до , но результат удвоен. Формула связывает изгибающий момент с величиной . Эта формула еще неудобна для практического использования, так как интеграл зависит от двух параметров .
Преобразуем эту формулу, приняв за переменную интеграции деформацию и обозначив деформацию крайнего волокна
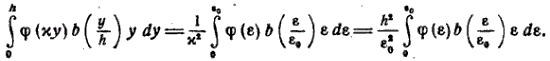
Положим
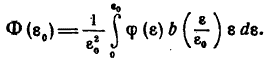
Тогда получим:
Имея график функции , можно вычислить функцию и построить для нее график.
В качестве примера рассмотрим изгиб стержня прямоугольного сечения при условии идеальной пластичности. В этом случае
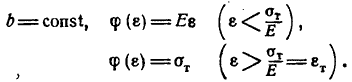
Пока
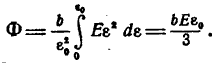
По формуле
Здесь h — полная высота, а не половина высоты. Отсюда
что совпадает с ранее найденным решением , если не обращать внимания на знак.
В области упруго-пластических деформаций
Поэтому
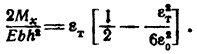
Построим график зависимости величины от безразмерного момента . Пока деформации всюду упруги, зависимость изображается прямой (107.3). Когда напряжение в крайнем волокне становится равным то есть состояние становится упруго-пластическим и вступает в действие формула (107.4). Соответственно график на рис. 156 становится криволинейным. При очень больших значениях безразмерный момент стремится к величине . Точка А на графике определяет тот момент, который соответствует началу текучести в крайней точке сечения, то есть признается опасным при расчете по допускаемым напряжениям.
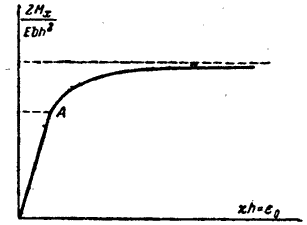
Как видно из графика, несущая способность стержня при этом еще не исчерпана, он еще сопротивляется изгибу. Полное исчерпание несущей способности происходит тогда, когда безразмерный момент возрастает до величины то есть становится больше на 33% по сравнению с моментом в точке А.
22. Кручение стержней. Внутренние усилия при кручении
Кручение испытывает стержень, нагруженный момен
тами, которые действуют в плоскостях, перпендикуляр
ных его продольной оси. Эти стержни называют валами.
В поперечных сечениях стержня возникает только одно
внутреннее усилие — крутящий момент Mz. Остальные
силовые факторы равны нулю.
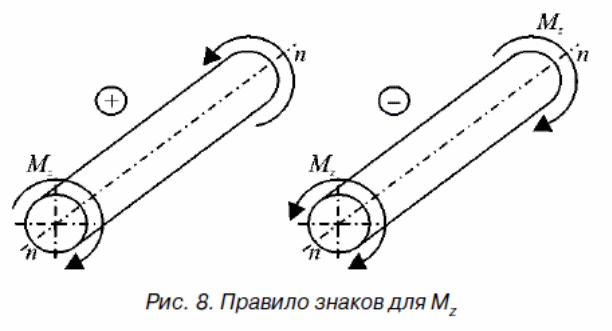
Крутящий момент можно считать положительным, если
при взгляде на сечение со стороны внешней нормали он
направлен по ходу часовой стрелки (рис. 8). Это правило
знаков необходимо для определения направления крутя
щего момента и для построения эпюры Mz. Положитель
ные значения крутящих моментов на эпюре будем от
кладывать вверх от горизонтальной базисной линии,
а отрицательные значения — вниз. Построение эпюры
крутящих моментов принципиально ничем не отличается
от построения эпюры продольных сил.
Также на стержень может действовать моментная на_
грузка интенсивностью mz. Между этой внешней мо_
ментной нагрузкой mz и крутящим моментом Mz имеет
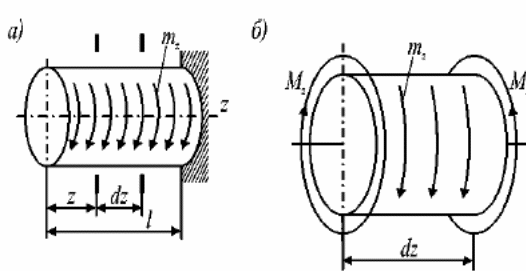
место дифференциальная зависимость. Пусть имеется стержень с моментной нагрузкой mz (рис. 9а), из
которого вырезан элемент длиной dz (рис. 9б).
Этот элемент нагружен уравновешивающими положи_
тельными крутящими моментами: в левом сечении —
Mz, в правом — Mz + dMz, причем dMz есть приращение
крутящего момента. Данный элемент также нагружен
внешней распределенной моментной нагрузкой mz (ее
можно считать равномерно распределенной ввиду ма_
лости dz). Уравнение равновесия для элемента:
Отсюда
