16. Współczynniki rozbieżności prognoz h.Theila

Udział najgorszego (statystycznego) typu błędu w ogólnej strukturze błędu

Błąd złego przewidywania skali zmienności zjawiska

Błąd, który mówi o przewidywaniu punktów zwrotnych

17. Zasady konstrukcji dwuskładnikowego portfela akcji w przypadku różnego skorelowania stóp zwrotu

WWA (wewn. Wartośc akcji)=f(x1 x2 ...) – czynniki determinujące wartość funkcji

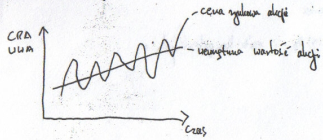
Analiza portfelowa (Markovitz): mając określony zasób funduszy oraz akcje do wyboru trzeba wybrać ile akcji jakiej firmy kupić następuje po analizie fundamentalnej.

Rt – stopa zwrotu z danej akcji w okresie t

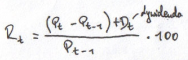
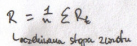
miara ryzyka inwestowania – odchylenie standardowe stopy zwrotu

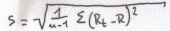
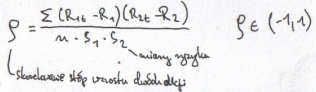
Portfel dwuskładnikowy (złożony z dwóch akcji)

w1+w2=1

Rp=w1R1+w2R2

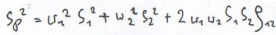
Ex:

R1=6%, R2=14%, S1=3%, S2=8%

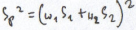
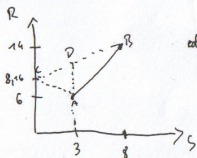
odcinek CD- oportunity set

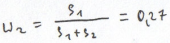
/Portfel z ryzykiem zerowym/

Rp=0,73*6+0,27*14=8,16

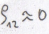
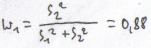
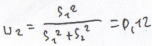
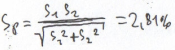
Sp- minimalne ryzyko portfela

Rp=6,96%

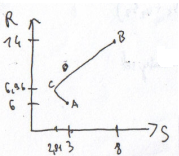
CD-oportunity set

18. Logitowe I przykłady ich zastosowania w praktyce gospodarczej

1.Określamy prawdopodobieństwo z jakim dany wariant zmiennej jakościowej występował w przeszłości w zależności od występowania innych czynników

2.Rozpatrujemy metody prognozowania zmiennych 0-1

_{Bujemy model opisujący oczekiwane wartości zmiennej Y}

_{Rosnąca funkcja kombinacji liniowej zmiennych x1,xn, składnika losowego (są to zmienne objaśniające czynniki wpływające na Y)}

_{W modelu legitowym f.F jest dystrybuantą rozkładu logistycznego.}

_{L-logit (funkcja odwrotna do F)}

_{Model legitowy stosuje się np. do oceny klienta w banku, który ubiega się o kredyt.}

19. Zasady obliczania I wykorzystania w prognozowaniu wskaźników sezonowości

Ustalamy wskaźniki sezonowości (o ile następuje wzrost lub spadek) nasilenia zjawiska w stosunku do poziomu przeciętnego.

j=1,2,3,…,m (numeracja sezonów)

i=1,2,3…,n (numeracja lat) N=n*m

Yt	t	Ct
Y1	1	C1
Y2	2	C2
…	…	…
Yn	N	CN

Trzeba stworzyć takie wskaźniki, które dla każdego sezonu podadzą relatywne do średniego poziomu wielkości wzrostu lub spadku zjawiska.

Grupujemy wskaźniki sezonowości:

	1	2	…	m
1	C1	C2		Cm
2	Cm+1	Cm+2		Cm+m
…
n	C(n-1)m+1			C(n-1)m+m=CN
	S1	S2	…	Sm

Wykorzystujemy wskaźniki do prognozowania danych kwartalnych