Дифференцирование и интегрирование решетчатых функций

Аналогом первой производной для решетчатой функции является либо первая прямая разность:

 f [n] = f [n+1] - f [n],

либо первая обратная разность:

 f [n] = f [n] - f [n-1].

Аналогов второй являются вторые разности. Прямая:

² f [n] =f [n+1] -  f [n] = (f [n+2] - f [n+1]) - (f [n+1] - f [n]) = f [n+2] - 2 f [n+1] + f [n],

и обратная:

² f [n] =  f [n] -f [n-1] = f [n] - 2 f [n-1] + f [n-2].

По аналогии могут определяться и высшие разности:

k f [n] = v=0k  (-1)vCkvf [n+k-v]

k f [n] = v=0k (-1)vCkvf [n-v]

где: C_k^v = k! / (v!(k-v)!).

Очевидно, что если f [n] определена только для положительных n, то для n=0 все обратные разности ^k f [n] равны нулю, что позволяет ...

Аналогом интеграла является неполная сумма:

 [n] = _m=0^n-1 f [m] = м₌₁ⁿ f [n-v],

и полная сумма:

_o[n] =  [n] + f [n].

Вопросы самоконтроля:

1. Как используется преобразование по Лапласу для исследования импульсных систем?

2. Дайте определение решетчатых функций.

Лекция 41 Исследование устойчивости системы по разностному уравнению

Цель лекции: изучение методов исследования устойчивости импульсных систем.

Аналогом ДУ для импульсной системы является уравнение в конечных разностях или разностное уравнение (РУ):

b₀^my[n] + b₁^m-1y[n] + ... + b_m y[n] = f [n],

(оно может быть составлено и в прямых разностях). Если раскрыть разности, то уравнение будет иметь вид:

a₀ y[n] + a₁ y[n-1] + ... + a_m y[n-m] = f [n],

где:

am-k = v=0k (-1)m-k bv Cm-vk-v ;

Cm-vk-v = (m-v)! / [ (k-v)! (m-k)! ] .

РУ легко машинизируются и для их расчета можно составлять рекуррентный алгоритм.

Учтем запаздывание передаточной функцией звена чистого запаздывания и вынесем теперь уже изображение дискретной последовательности y[n] в уравнении (1) за скобку:

(a₀ + a₁e^-Ts + ... + a_me^-mTs) Y ^*[s] = F ^*[s],

введем обозначение z = e^Ts и перепишем уравнение:

(a₀ + a₁ z ^-1 + ... + a_m z ^-m) Y [z] = F [z].

Решая для него ХУ (левая часть приравненная к нулю) можно получить "Общее решение" - т.е. переходную составляющую:

y [n] = С₁ z₁ⁿ + С₂ z₂ⁿ + ... +  С_m z_mⁿ ,

где: z₁, z₂, ..., z_m - корни ХУ; а C_i - произвольные постоянные.

Вид решения ХУ определяет условие устойчивости для систем, описанных с помощью РУ:

| z_i | < 1.

Критерий устойчивости импульсных систем

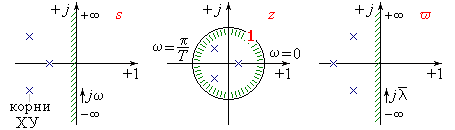
Построим область устойчивости в плоскости комплексной величины z. Воспользуемся методикой D-разбиения и, меняя частоту w от -  до +  , получим границу z = e^Ts = e ^jwT - в виде окружности единичного радиуса, внутрь которой попадает левая полуплоскость комплексной величины s. Следовательно, для устойчивости, все корни-полюсы замкнутой системы Ф(z) должны находится внутри этой окружности.

Итак, для описанных с помощью аппарата Z-преобразования импульсных систем, всилу изменившегося вида области устойчивости и периодичности их ЧХ W(e ^jwT), разработанные для непрерывных систем критери устойчивости (кроме критерия Найквиста и корневого годографа), а так же наиболее эффективные методы коррекции и синтеза (использующие ЛАЧХ & ЛФЧХ) не приемлемы.

Для преодоления этого затруднения используют -преобразование, которое отражает окружность единичного радиуса на мнимую ось комплексной величины , с помощью подстановки:

.

Физически подстановка означает переход к ДУ заменой в РУ элементов чистого запаздывания грубой аппроксимацией - одним фазосдвигающим звеном.

Вторая формула для перехода в область псевдочастот  получена из соотношения:

,

отметим так же, что:

.

-Домен и домен псевдочастоты  используют редко, поскольку для большинства импульсных и цифровых систем частота дискретизации 1/T выбирается в 6...10 раз больше частоты среза. В таком случае выполняется условие _срT<2, вследствие чего в полосе системы псевдочастота  и частота  практически совпадают. Поэтому обходятся доменом обычных частот, а для переходов используют формулы "Билинейного преобразования":

.

Вопросы самоконтроля:

1. Как получить разностное уравнение в реальном масштабе времени из характеристического уравнения систем?

2. Дайте определение критерию устойчивости импульсных систем.

3. Перечислите порядок проведения Z-преобразований.

4. Каким образом перейти от Z-формы к псевдочастоте для дальнейшего исследования импульсной системы?

5. Перечислите порядок проведения билинейного преобразования?