1.4 Основные законы управления
Законом управления называют математическую зависимость, в соответствии с которой управляющее воздействие на объект вырабатывалось бы безынерционным управляющим устройством.
В технике используют довольно много различных законов управления. Закон управления тесно связан с конструкцией управляющего устройства, и одним из распространенных видов классификации регуляторов является классификация по законам управления.
Ограничимся
упоминанием о наиболее распространенных
законах, реализуемых линейными
регуляторами. В этих простейших законах
управляющее воздействие линейно зависит
от отклонения, его интеграла и первой
производной по времени. При описании
законов наиболее удобно использовать
безразмерные относительные переменные
,
,
где
и
—
базовые значения (например, соответствующие
номинальному режиму объекта).
Пропорциональный
закон (обозначаемый П):
.
Регулятор, осуществляющий этот закон,
называют пропорциональным. Постоянную
называют
коэффициентом передачи (усиления)
регулятора, обратную величину — статизмом
регулятора. С возрастанием статизма
регулятора возрастает и статизм
регулирования.
Интегральный закон (И): |
|
, или |
|
.Постоянная Т имеет размерность времени и ее называют постоянной времени интегрирования. Интегральный регулятор — астатический и именно с его помощью осуществляется рассмотренная выше простейшая схема астатического регулирования.
Пропорционально-интегральный закон (ПИ): |
|
.Иногда его называют пропорциональным законом с интегральной коррекцией. Регулятор ПИ также обеспечивает астатическое регулирование. В этом можно убедиться, представив уравнение в виде
.
В состоянии
равновесия при постоянных воздействиях
должно быть
,
,
откуда равновесие может иметь место
лишь при
.
Пропорционально-интегрально-дифференциальный закон (ПИД):
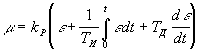
Постоянные Ти и
Тд соответственно называют постоянными
времени интегрирования и дифференцирования.
Регулятор ПИД также обеспечивает
астатическое регулирование. Производную
вводят
в закон регулирования для повышения
качества процесса регулирования.
2 Математическое описание автоматических систем управления
На определенном этапе разработки и исследования автоматической системы управления получают ее математическое описание — описание процессов, проистекающих в системе, на языке математики. Математическое описание может быть аналитическим (с помощью уравнений), графическим (с помощью графиков, структурных схем и графов) и табличным (с помощью таблиц).
Во многих автоматических системах процессы описываются дифференциальными, разностными, дифференциально-разностными, интегральными и интегро-дифференциальными уравнениями. Рассмотрим построение математической модели систем, которые могут быть описаны обыкновенными дифференциальными уравнениями.
2.1 Уравнения динамики и статики. Линеаризация
В общем случае звенья и системы описывают нелинейными дифференциальными уравнениями произвольного порядка. Под звеном понимается математическая модель элемента. Для примера рассмотрим звено (рис. 2.1), которое можно описать дифференциальным уравнением второго порядка
|
(2.1) |
где у — выходная
величина,
и
—
входные величины,
и
—первые
производные по времени,
—
вторая производная по времени.
Уравнение (2.1),
описывающее процессы в звене при
произвольных входных воздействиях
называют уравнением
динамики.
Пусть при постоянных входных величинах
и
процесс
в звене с течением времени установится:
выходная величина примет постоянное
значение
.
Тогда (2.1) примет вид
|
(2.2) |
Это уравнение описывает статический или установившийся режим и его называют уравнением статики.
Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой звена или элемента (а также системы) называют зависимость выходной величины от входной в статическом режиме. Статическую характеристику можно построить экспериментально, подавая на вход элемента постоянное воздействие и измеряя выходную величину после окончания переходного процесса, или расчетным путем, используя уравнение статики.
Если звено имеет несколько входов, то оно описывается с помощью семейства статических характеристик.
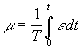
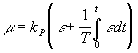