4.5. Корневые методы оценки качества регулирования
Из § 4.2. известно, что характер переходного процесса в системе определяют по ее реакции на единичное ступенчатое воздействие. Переходная характеристика h(t) системы может быть вычислена при помощи обратного преобразования Лапласа (по формулам разложения Хевисайда)
.
Если D(s) не имеет кратных корней, то
,
(4.13)
где Si — корни характеристического полинома замкнутой системы D(s) = о; D'(Si) =dD(s)/ds— первая производная характеристического полинома D(s) по s при s = Si.
Из (4.13) видно, что
на характер переходного процесса влияют
и числитель и знаменатель передаточной
функции замкнутой системы
.
Если числитель
не
имеет нулей, т.е. представляет собой
постоянную величину, то характер
переходных процессов можно оценивать
по ее полюсам, т.е. корням характеристического
уравнения замкнутой системы D(s)
== 0.
А.А. Фельдбаумом в [16] введена следующая
классификация распределения корней
характеристического уравнения:
класс “0” — все корни вещественные;
класс “1” — среди корней есть одна пара комплексных сопряженных;
класс “II” — среди корней есть две пары комплексных сопряженных.
Для приближенной оценки качества переходного процесса в системе нужно на плоскости корней s выделить ту область, где располагаются корни ее характеристического уравнения (рис. 4.7).
Рис. 4.7
Область ABCD ограничена дугами AD и СВ, радиусы которых АО и 0В соответственно равны наименьшему модулю корней ( m = ОА) и наибольшему (М = 0В) и отрезками CD и АВ лучей ОС и O В, образующих угол ф, внутри которого располагаются все корни. Так как вычисление модулей корней может представлять затруднения, то эту область чаще всего представляют трапецией (рис. 4.8).
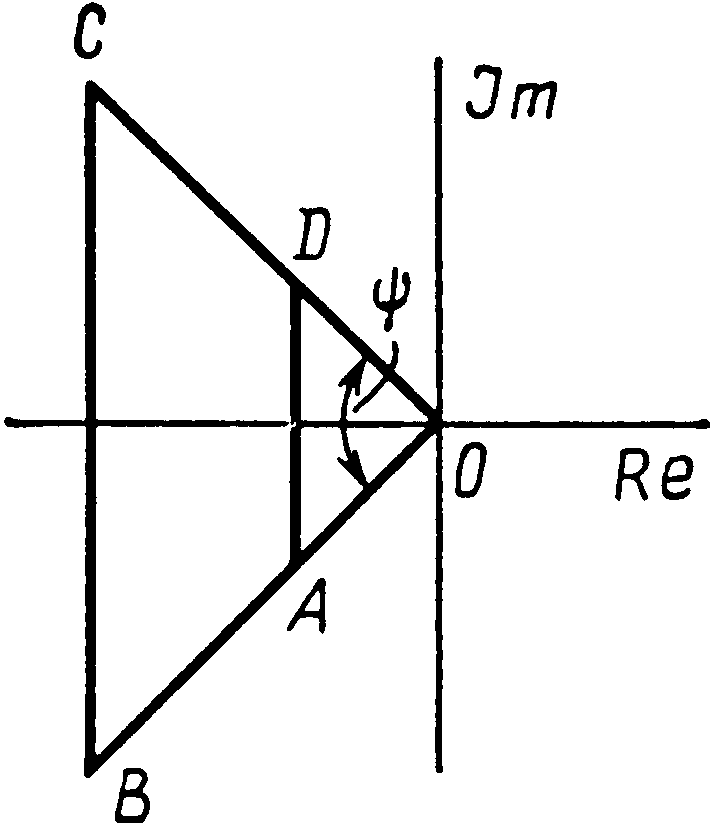
Рис. 4.8
Все корни характеристического уравнения системы располагаются внутри этой трапеции, на ее сторонах и основаниях хотя бы по одному корню, а вне ее — ни одного. Понятие степени устойчивости введено Я.3. Цыпкиным и П.В. Бромбергом [181. Степенью устойчивости h называют расстояние от мнимой оси до ближайшего корня или ближайшей пары сопряженных комплексных корней. Степень устойчивости h определяет ближайшее к мнимой оси основание трапеции AD (рис. 4.8).
Колебательностью системы m [16] называют тангенс угла, образованного отрицательной вещественной полуосью и лучом из начала координат к корню, у которого отношение мнимой части к действительной максимально
,
(4.14)
где
—
значение мнимой части корней
;
—
действительная часть.
Существуют способы
определения границ области, где
располагаются корни характеристического
уравнения. Например, можно использовать
теорему Какейя: если коэффициенты
характеристического
уравнения
положительны и
если все отношения последующего
коэффициента уравнения (
)
к предыдущему (
)
,
располагаются между положительными
числами т
и М
(m>0,
M>0,
m<
<M),
где i ==
0,1, ...n,
то и модули всех корней D(s)
заключены тоже между числами т
и М,
т. е.
.
(4.15)
Другой способ заключается в определении верхней границы М модулей корней характеристического уравнения
,
(4.16)
где
—
наибольший коэффициент уравнения.
Поскольку рассмотренные методы дают слишком широкие границы области расположения корней на комплексной плоскости, в чем нетрудно убедиться на простых примерах, то чаще всего область распределения корней определяют вычислением степени устойчивости, колебательности и максимального удаления корня от мнимой оси.
Степень устойчивости. Пусть общее решение дифференциального уравнения системы
,
(4.17)
где Si — корни характеристического уравнения D(s) = 0. Составляющая этого решения, определяемая степенью устойчивости, запишется в виде
(4.18)
для случая класса 0 корней, или
(4.19)
для случая 1-го класса корней.
В большинстве
случаев переходный процесс можно считать
закончившимся тогда, когда затухнет
составляющая переходного процесса,
определяемая степенью устойчивости,
т.е. порядок величины времени затухания
процесса можно грубо оценить по наиболее
медленно затухающей составляющей
[(4.18),
(4.19)]. В случае, когда ближайшим к мнимой
оси является вещественный корень, из
(4.18) можно получить следующую зависимость:
.
Если принять,
например,
,
то время переходного процесса
.
В том случае, когда
ближайшей к мнимой оси является пара
комплексных корней, из (4.19) можно найти
верхнюю границу времени переходного
процесса
.
Можно поставить две задачи:
По заданным параметрам системы — коэффициентам D(s)— определить степень устойчивости системы (задача анализа степени устойчивости).
По заданной степени устойчивости определить значение варьируемых параметров системы (задача синтеза заданной степени устойчивости).
Воспользуемся
методом, изложенным в [18]. Предлагается
сместить мнимую ось влево на величину
h , тогда один корень окажется на мнимой
оси, а система на границе устойчивости.
Это соответствует обращению в нуль
старшего определителя Гурвица
.
Это условие дает уравнение, по которому,
задаваясь коэффициентами уравнения,
можно определить h или решить обратную
задачу.
Пусть характеристическое уравнение системы
.
Введем новую
переменную
,
подставив значение
в
уравнение D(s)
= 0, получим новое смещенное уравнение
,
(4.20)
где
.
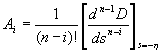(4.21)
Если в смещенном
уравнении окажется
,
то ближайшим к мнимой оси окажется
нулевой корень, если
,
то пара сопряженных комплексных корней.
Условие границы
устойчивости для системы, описанной
уравнением (4.20), по критерию Гурвица
при
соблюдении всех остальных условий
устойчивости Гурвица. Теперь можно
решать одну из поставленных выше задач.
Колебательность системы.
Если корни
характеристического уравнения системы
,
то
.
(4.30)
Подобно тому как по заданным параметрам CAP определялась степень устойчивости h (и наоборот), можно определять значение колебательности m , при известных параметрах системы (и решать обратную задачу) [16].
Для этого в
характеристическое уравнение системы
вводится замена
,
равноценная повороту мнимой оси на угол
(
),
при этом пара сопряженных комплексных
корней окажется на мнимой оси, а фиктивная
система — на границе устойчивости.
Колебательность m является оценкой
переходного процесса сверху, при
увеличении m возрастает число колебаний
п
за время регулирования и возрастает
перерегулирование. Реальный переходной
процесс может иметь значительно лучшее
качество. Запишем смещенное
характеристическое уравнение
, (4.31)
где
.
(4.32)
В (4.31) часть
коэффициентов — комплексные числа.
Поскольку фиктивная система находится
на границе устойчивости, то (4.31) имеет
пару сопряженных мнимых корней
.
Если в (4.31) вместо
подставить
и
разделить смещенный характеристический
полином на мнимую и действительную
часть, то их можно поочередно приравнять
нулю, получив при этом систему двух
уравнений
.
Исключив из этой
системы
,
получим искомое значение
и
.