Лабораторная работа № 8 Реализация формул Ньютона-Котеса на эвм

Задание 1:

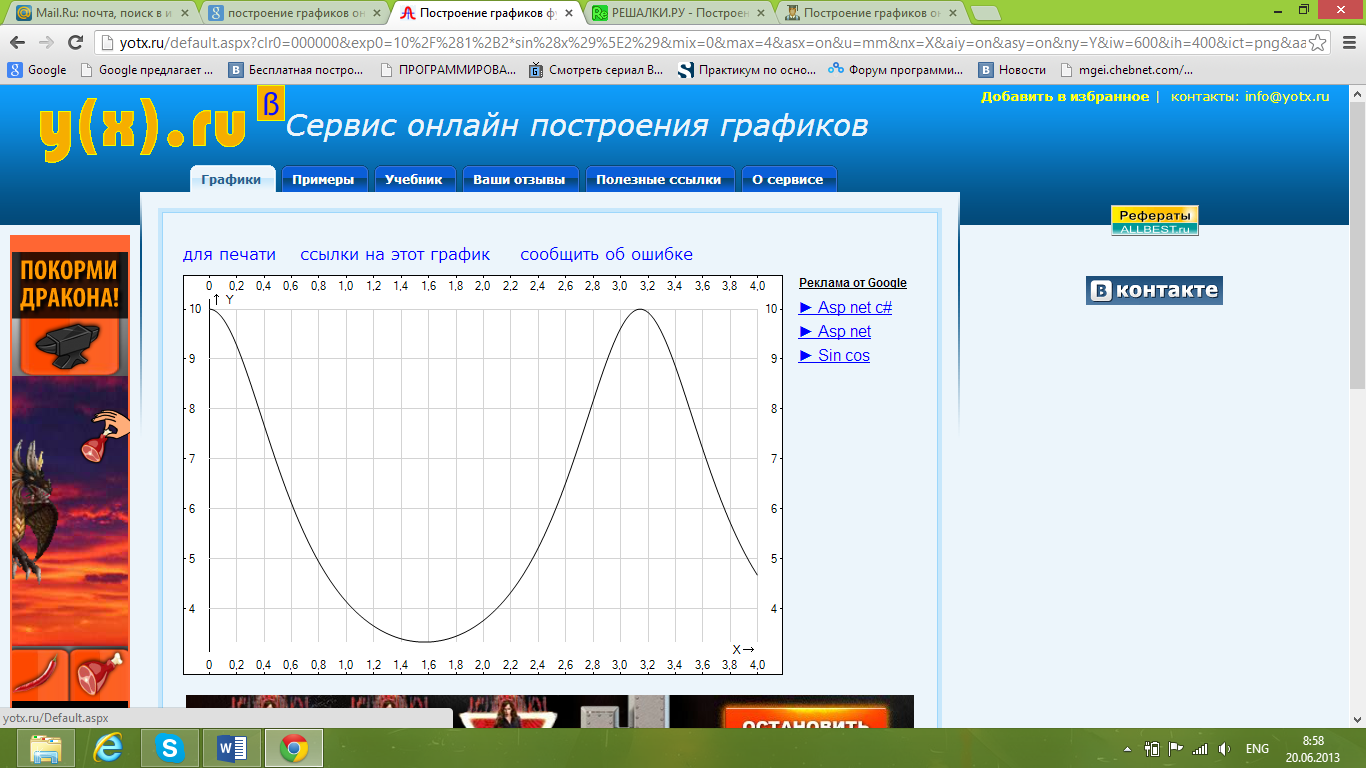
С помощью программ на ЭВМ вычислить значение интеграла заданной функции на отрезке по формуле Симпсона методом половинного счета с точностью 10^-6

[3,4]

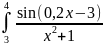
Ход работы:

Program prim1;

Uses crt;

const n=10;

type mas=array[0..n] of real;

var y:mas;

a,b,S,Integral,h,x:real;

i:integer;

begin

clrscr;

writeln('Введите границы отрезка интегрирования ');

readln(a,b);

writeln('Задайте величину шага интегрирования ');

readln(h);

x:=h;

for i:=0 to n do

begin

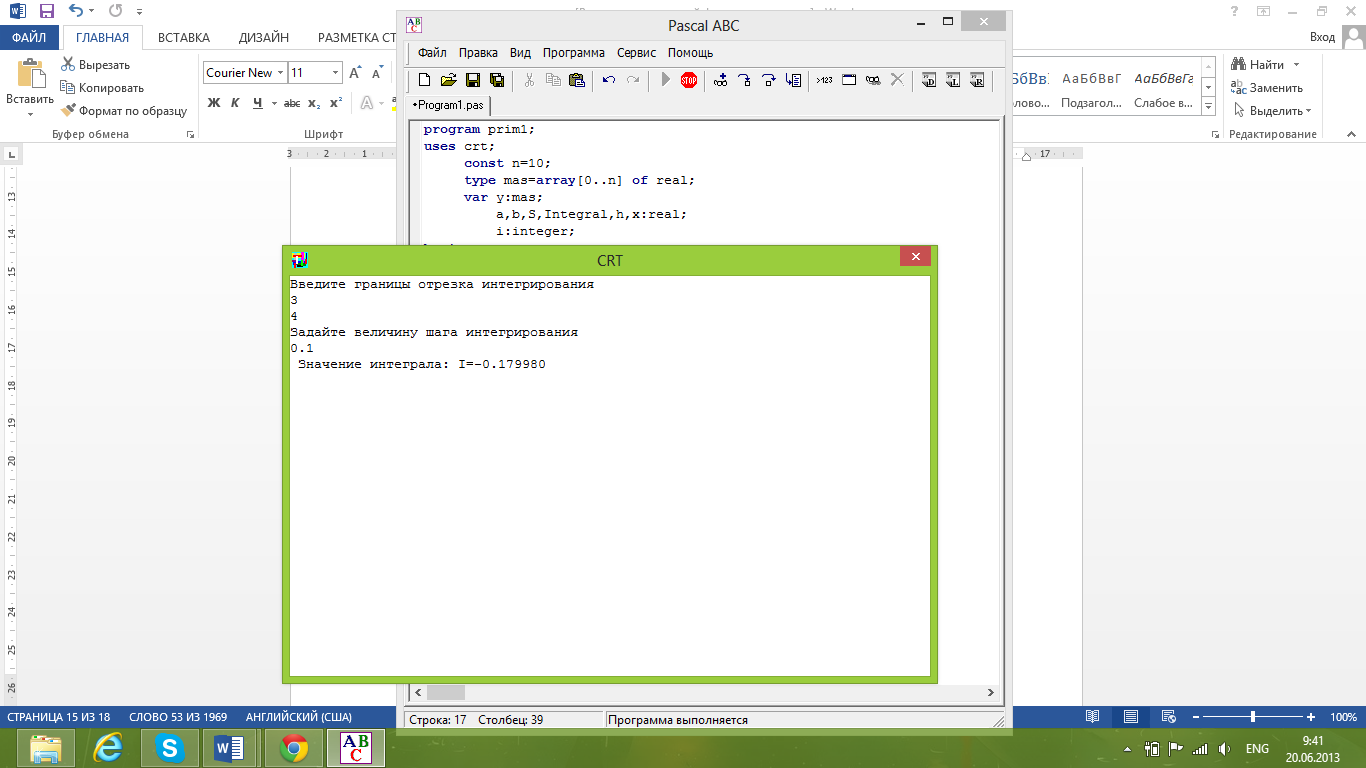
y[i]:=((sin(0.2*x-3))/(sqr(x)+1)

x:=x+h;

end;

s:=(y[0]-y[n])/2;

i:=1;

repeat

s:=s+(2*y[i]+y[i+1]);

i:=i+2;

until i>=n;

Integral:=2*(b-a)*s/(3*n);

writeln (' Значение интеграла: I=',Integral:3:6);

readln;

end.

Лабораторная работа №9

Метод Эйлера для решения ОДУ

Задание :

Решить дифференциальное уравнение (1) с начальным условием (2) методом Эйлера, усовершенствованным методом Эйлера и методом Рунге-Кутта. Расчет провести на отрезке [с,d] дважды: с шагом 0,1 и 0,05. Сделать оценку погрешности полученного решения в точке d методом двойного просчета.

y' =1+0,4y sin x-1,5y² x0 1 y(0)=0

Ход работы:

Метод Эйлера

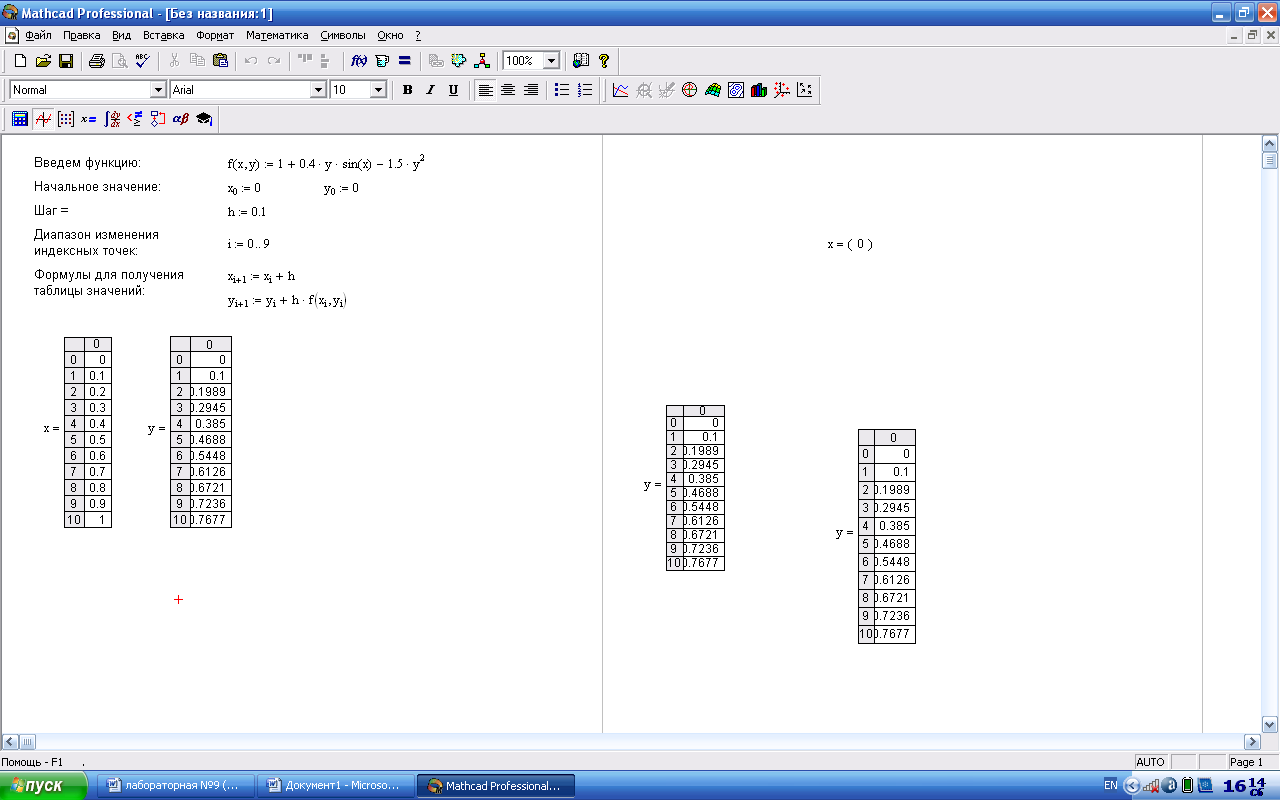
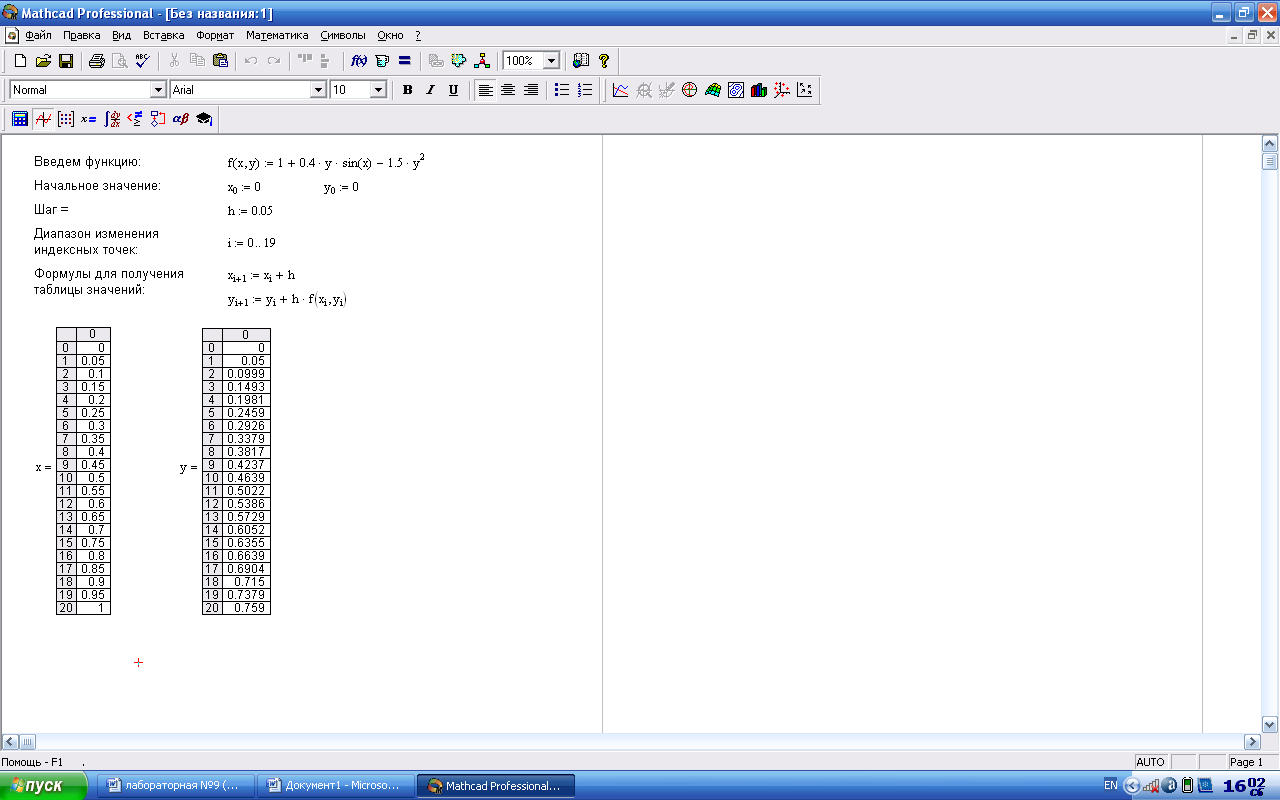
Метод Рунге-Кутта

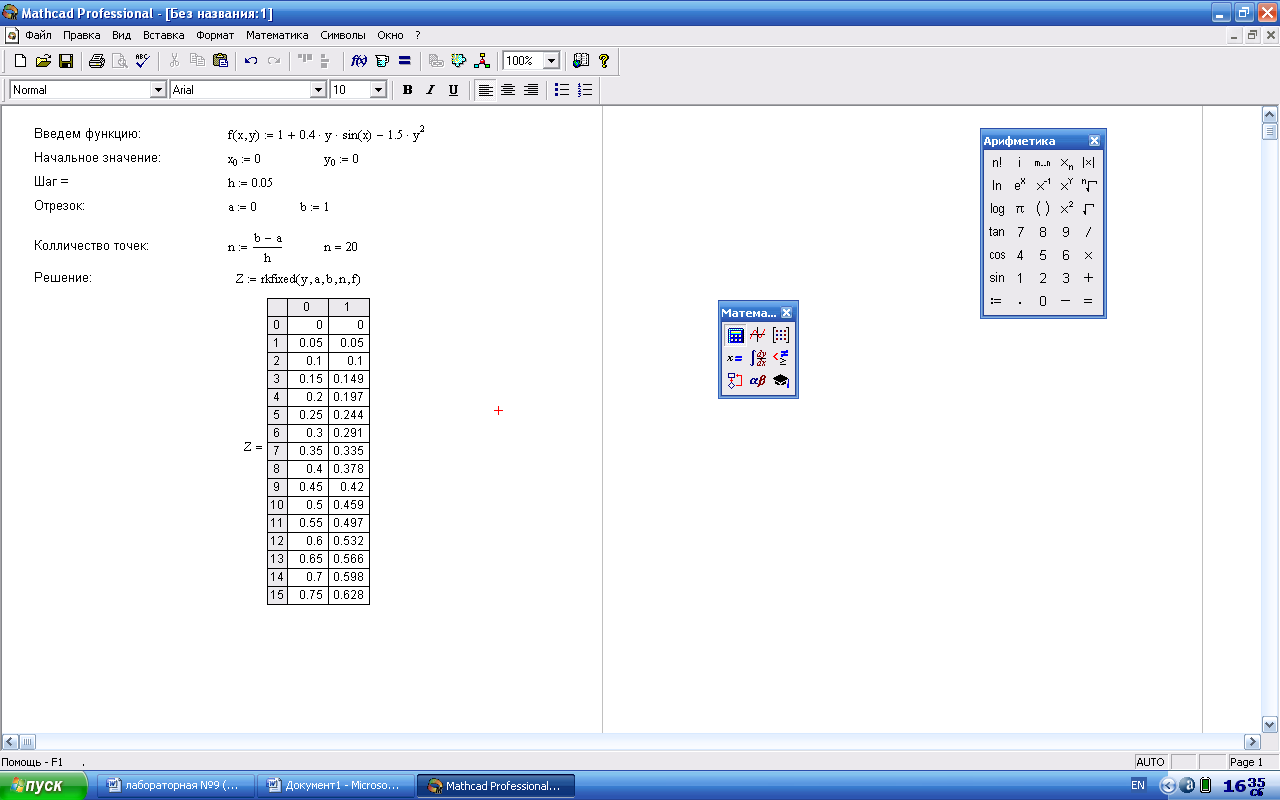
Лабораторная работа №10

Метод золотого сечения для решения задачи одномерной оптимизации

Найдите минимум функции f(x) на указанном отрезке.

1. «вручную» с точностью, доступной за 2 шага вычислительного процесса;

2. с помощью программ для ЭВМ с точностью 1*10^-6

Ход работы:

[0;4]

1. - пропорция золотого сечения.

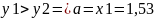
|b-a| < =>